
已知四棱锥S-ABCD的底面是边长为6的正方形,SA⊥底面ABCD,且SA=8,M是SA的中点,过M和BC作截面交SD于N.
(1)求证:截面MBCN是梯形,并求截面的面积;
(2)求截面MBCN与底面ABCD的夹角α.
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知四棱锥S-ABCD中,四边形ABCD是直角梯形,∠ABC=∠BAD=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=
已知四棱锥S-ABCD中,四边形ABCD是直角梯形,∠ABC=∠BAD=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源:101网校同步练习 高一数学 苏教版(新课标·2004年初审) 苏教版 题型:022
已知三棱锥S-ABC的三条侧棱两两垂直,SA=5,SB=4,SC=3,D为AB中点,E为AC中点,则四棱锥S-BCED的体积为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年安徽信息交流)已知三棱锥S―ABC的四个顶点在以O为球心的同一球面上,且SA=SB=SC=AB,∠ACB=90。,则当球的表面积为400![]() 时。点O到平面ABC的距离为 ( )
时。点O到平面ABC的距离为 ( )
A.4 B.5 C.6 D.8
查看答案和解析>>
科目:高中数学 来源:福建省09-10学年高二下学期期末数学理科考试试题 题型:解答题
(本小题满分13分)
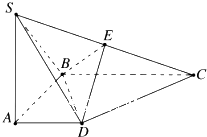
如图,已知四棱锥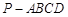 的底面是直角梯形,∠ABC
的底面是直角梯形,∠ABC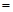 ∠BCD
∠BCD 90°,AB
90°,AB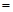 BC
BC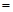 PB
PB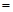 PC
PC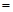 2CD
2CD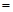 2,侧面PBC⊥底面ABCD。
2,侧面PBC⊥底面ABCD。
(1)求证: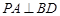 ;K^S*5U.C#O%
;K^S*5U.C#O%
(2)求二面角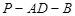 的余弦值。
的余弦值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com