
【题目】已知圆![]() 圆心坐标为点
圆心坐标为点![]() 为坐标原点,
为坐标原点,![]() 轴、
轴、![]() 轴被圆
轴被圆![]() 截得的弦分别为
截得的弦分别为![]() 、
、![]() .
.
(1)证明:![]() 的面积为定值;
的面积为定值;
(2)设直线![]() 与圆
与圆![]() 交于
交于![]() 两点,若
两点,若![]() ,求圆
,求圆![]() 的方程.
的方程.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)利用几何条件可知,![]() 为直角三角形,且圆过原点,所以得知三角形两直角边边长,求得面积;
为直角三角形,且圆过原点,所以得知三角形两直角边边长,求得面积;
(2)由![]() 及原点O在圆上,知OC
及原点O在圆上,知OC![]() MN,所以
MN,所以![]() ,求出
,求出![]() 的值,再利用直线与圆的位置关系判断检验,符合题意的解,最后写出圆
的值,再利用直线与圆的位置关系判断检验,符合题意的解,最后写出圆![]() 的方程。
的方程。
(1)因为![]() 轴、
轴、![]() 轴被圆
轴被圆![]() 截得的弦分别为
截得的弦分别为![]() 、
、![]() ,
,
所以![]() 经过
经过![]() ,又
,又![]() 为
为![]() 中点,所以
中点,所以![]() ,所以
,所以
![]() ,所以
,所以![]() 的面积为定值.
的面积为定值.
(2)因为直线![]() 与圆
与圆![]() 交于
交于![]() 两点,
两点,![]() ,
,
所以![]() 的中垂线经过
的中垂线经过![]() ,且过
,且过![]() ,所以
,所以![]() 的方程
的方程![]() ,
,
所以![]() ,所以当
,所以当![]() 时,有圆心
时,有圆心![]() ,半径
,半径![]() ,
,
所以圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
所以直线![]() 与圆
与圆![]() 交于点
交于点![]() 两点,故成立;
两点,故成立;
当![]() 时,有圆心
时,有圆心![]() ,半径
,半径![]() ,所以圆心
,所以圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,所以直线
,所以直线![]() 与圆
与圆![]() 不相交,故
不相交,故![]() (舍去),
(舍去),
综上所述,圆![]() 的方程为
的方程为![]() .
.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:
【题目】已知正三棱锥P﹣ABC中E,F分别是AC,PC的中点,若EF⊥BF,AB=2,则三棱锥P﹣ABC的外接球的表面积( )
A.4π
B.6π
C.8π
D.12π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:

(1)求回归直线方程![]() ,其中
,其中![]() ,
,![]() .
.
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学40名数学教师,按年龄从小到大编号为1,2,…40。现从中任意选取6人分成两组分配到A,B两所学校从事支教工作,其中三名编号较小的教师在一组,三名编号较大的教师在另一组,那么编号为8,12,28的数学教师同时入选并被分配到同一所学校的方法种数是
A. 220 B. 440 C. 255 D. 510
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司新上一条生产线,为保证新的生产线正常工作,需对该生产线进行检测,现从该生产线上随机抽取100件产品,测量产品数据,用统计方法得到样本的平均数![]() ,标准差
,标准差![]() ,绘制如图所示的频率分布直方图,以频率值作为概率估值。
,绘制如图所示的频率分布直方图,以频率值作为概率估值。
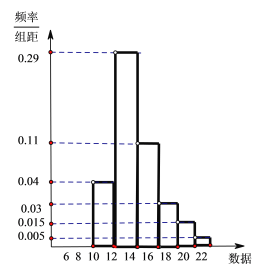
(1)从该生产线加工的产品中任意抽取一件,记其数据为![]() ,依据以下不等式评判(
,依据以下不等式评判(![]() 表示对应事件的概率)
表示对应事件的概率)
①![]()
②![]()
③![]()
评判规则为:若至少满足以上两个不等式,则生产状况为优,无需检修;否则需检修生产线,试判断该生产线是否需要检修;
(2)将数据不在![]() 内的产品视为次品,从该生产线加工的产品中任意抽取2件,次品数记为
内的产品视为次品,从该生产线加工的产品中任意抽取2件,次品数记为![]() ,求
,求![]() 的分布列与数学期望
的分布列与数学期望![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极点与直角坐标系的原点重合,极轴与x轴的正半轴重合,圆C的极坐标方程是ρ=asinθ,直线l的参数方程是  (t为参数)
(t为参数)
(1)若a=2,直线l与x轴的交点是M,N是圆C上一动点,求|MN|的最大值;
(2)直线l被圆C截得的弦长等于圆C的半径的 ![]() 倍,求a的值.
倍,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com