
| A. | $\frac{1}{4}$ | B. | -3 | C. | $\frac{2}{3}$ | D. | -2 |
分析 a1=$\frac{1}{4}$,an+1=1-$\frac{1}{a_n}$,可得a2=-3,a3=$\frac{4}{3}$,a4=$\frac{1}{4}$,…,可得an+3=an.利用周期性即可得出.
解答 解:∵a1=$\frac{1}{4}$,an+1=1-$\frac{1}{a_n}$,
∴a2=1-4=-3,a3=$1-\frac{1}{-3}$=$\frac{4}{3}$,a4=1-$\frac{1}{\frac{4}{3}}$=$\frac{1}{4}$,
…,
可得an+3=an.
∴a2015=a671×3+2=a2=-3.
故选:B.
点评 本题考查了数列的递推关系、周期性,考查了推理能力与计算能力,属于中档题.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | 250 | B. | -250 | C. | 150 | D. | -150 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
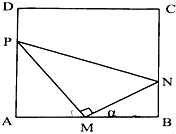 上海迪士尼乐园有一块长方形地ABCD,若要在此地块上拟建一个Rt△MNP的主题乐园,已知AB=2km,AD=$\sqrt{3}$km,点M是AB的中点,点P在线段AD上,点N在线段BC上,记∠NMB=α.
上海迪士尼乐园有一块长方形地ABCD,若要在此地块上拟建一个Rt△MNP的主题乐园,已知AB=2km,AD=$\sqrt{3}$km,点M是AB的中点,点P在线段AD上,点N在线段BC上,记∠NMB=α.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
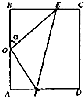 某休闲农庄有一块长方形鱼塘ABCD,AB=100米,BC=50$\sqrt{3}$米,为了便于游客休闲散步,该农庄决定在鱼塘内建3条如图所示的观光走廊OE、EF和OF,考虑到整体规划,要求O是AB的中点,点E在边BC上,点F在边AD上(不含顶点),且∠EOF=90°.($\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
某休闲农庄有一块长方形鱼塘ABCD,AB=100米,BC=50$\sqrt{3}$米,为了便于游客休闲散步,该农庄决定在鱼塘内建3条如图所示的观光走廊OE、EF和OF,考虑到整体规划,要求O是AB的中点,点E在边BC上,点F在边AD上(不含顶点),且∠EOF=90°.($\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
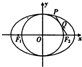 如图,已知F1,F2是椭圆C:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的左右焦点,点P在椭圆C上,线段PF2与圆x2+y2=b2相切于点Q,若点Q为线段PF2的中点,则b的值为( )
如图,已知F1,F2是椭圆C:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的左右焦点,点P在椭圆C上,线段PF2与圆x2+y2=b2相切于点Q,若点Q为线段PF2的中点,则b的值为( )| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{6}$ | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2 | B. | 2x2 | C. | 2x2+2 | D. | x2+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com