
 如图,底角∠ABE=45°的直角梯形ABCD,底边BC长为4cm,腰长AB为$2\sqrt{2}$cm,当一条垂直于底边BC的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BE=x,试写出阴影部分的面积y与x的函数关系式,并画出函数大致图象.
如图,底角∠ABE=45°的直角梯形ABCD,底边BC长为4cm,腰长AB为$2\sqrt{2}$cm,当一条垂直于底边BC的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BE=x,试写出阴影部分的面积y与x的函数关系式,并画出函数大致图象. 分析 当直线l过点A时,BE=AB•cos45°=2,∴当x=0时,阴影部分为一点;当0<x≤2时,阴影部分为等腰直角三角形;当2<x≤4时,阴影部分为直角边为2的等腰直角三角形加矩形,矩形相临两边长分别为x-2和2.
解答 解:当直线l过点A时,BE=AB•cos45°=2,
∴当x=0时,y=0;
当0<x≤2时,y=$\frac{1}{2}$x2;
当2<x≤4时,y=$\frac{1}{2}$•22+2(x-2)=2x-2.
∴y=$\left\{\begin{array}{l}{\frac{1}{2}{x}^{2},0≤x≤2}\\{2x-2,2<x≤4}\end{array}\right.$.
函数图象为: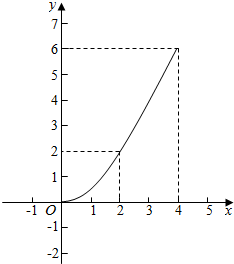
点评 本题考查了分段函数的解析式与图象,根据题意找到x的分界点及范围是关键,属于基础题.


 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(2a)<f(-a) | B. | f(π)>f(-3) | C. | $f(-\frac{{\sqrt{3}}}{2})<f(\frac{4}{5})$ | D. | f(a2+1)<f(1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜爱 | 不喜爱 | 合计 | |
| 男生 | 5 | ||
| 女生 | 10 | ||
| 合计 | 50 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com