
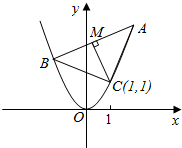
 过抛物线y=x2上定点C(1,1)引两条互相垂直的弦CA、CB,作CM⊥AB,M为垂足,求点M的轨迹方程.
过抛物线y=x2上定点C(1,1)引两条互相垂直的弦CA、CB,作CM⊥AB,M为垂足,求点M的轨迹方程. 分析 确定直线AB过定点D(-1,2),又CM⊥AB,可得点M在以CD为直径的圆上,即可求点M的轨迹方程.
解答  解:设A(m,m2),B(n,n2),则直线AB方程为:$\frac{{y-{n^2}}}{{{m^2}-{n^2}}}=\frac{x-n}{m-n}$
解:设A(m,m2),B(n,n2),则直线AB方程为:$\frac{{y-{n^2}}}{{{m^2}-{n^2}}}=\frac{x-n}{m-n}$
即y=(m+n)x-mn,
∵CA⊥CB,
∴${k_{AC}}•{k_{BC}}=\frac{{{m^2}-1}}{m-1}•\frac{{{n^2}-1}}{n-1}=(m+1)(n+1)=-1$
即m+n+mn=-2,
故直线AB方程为:y=(m+n)x+m+n+2
即y=(m+n)(x+1)+2,
∴直线AB过定点D(-1,2),
又CM⊥AB
∴点M在以CD为直径的圆上,其方程为:${x^2}+{(y-\frac{3}{2})^2}=\frac{5}{4}$
点评 本题考查轨迹方程,考查学生的计算能力,确定直线AB过定点D(-1,2)是关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1<m<3 | B. | -3<m<-1 | C. | 1<m<3 | D. | 2<m<3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com