
【题目】如图,在三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,点
的中点,点![]() 在平面
在平面![]() 内的射影在线段
内的射影在线段![]() 上.
上.
(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() 是正三角形,求二面角
是正三角形,求二面角![]() 的余弦值.
的余弦值.

科目:高中数学 来源: 题型:
【题目】某电动汽车“行车数据”的两次记录如下表:
记录时间 | 累计里程 (单位:公里) | 平均耗电量(单位: | 剩余续航里程 (单位:公里) |
2019年1月1日 | 4000 | 0.125 | 280 |
2019年1月2日 | 4100 | 0.126 | 146 |
(注:累计里程指汽车从出厂开始累计行驶的路程,累计耗电量指汽车从出厂开始累计消耗的电量,平均耗电量=![]() ,剩余续航里程=
,剩余续航里程=![]() ,下面对该车在两次记录时间段内行驶100公里的耗电量估计正确的是
,下面对该车在两次记录时间段内行驶100公里的耗电量估计正确的是
A. 等于12.5B. 12.5到12.6之间
C. 等于12.6D. 大于12.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 、
、![]() 是定义在实数集
是定义在实数集![]() 上的实值函数,如果存在
上的实值函数,如果存在![]() ,使得对任何
,使得对任何![]() ,都有
,都有![]() ,那么称
,那么称![]() 比
比![]() 高兴,如果对任何
高兴,如果对任何![]() ,都存在
,都存在![]() ,使得
,使得![]() ,那么称
,那么称![]() 比
比![]() 幸运,对于实数
幸运,对于实数![]() 和上述函数
和上述函数![]() ,定义
,定义![]() .
.
(1)①![]() ,
,![]() ,判断
,判断![]() 是否比
是否比![]() 高兴?
高兴?
②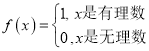 ,
,![]() ,判断
,判断![]() 是否比
是否比![]() 幸运?
幸运?
(2)判断下列命题是否正确?并说明理由:
①如果![]() 比
比![]() 高兴,
高兴,![]() 比
比![]() 高兴,那么
高兴,那么![]() 比
比![]() 高兴;
高兴;
②如果![]() 比
比![]() 幸运,
幸运,![]() 比
比![]() 幸运,那么
幸运,那么![]() 比
比![]() 幸运;
幸运;
(3)证明:对每个函数![]() ,均存在函数
,均存在函数![]() ,使得对任何实数
,使得对任何实数![]() ,
,![]() 都比
都比![]() 幸运,
幸运,![]() 也比
也比![]() 幸运.
幸运.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,四边形
,四边形![]() 为矩形,且
为矩形,且![]() 平面
平面![]() ,
,![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)点![]() 在线段
在线段![]() 上运动,当点
上运动,当点![]() 在什么位置时,平面
在什么位置时,平面![]() 与平面
与平面![]() 所成锐二面角最大,并求此时二面角的余弦值.
所成锐二面角最大,并求此时二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中医药,是包括汉族和少数民族医药在内的我国各民族医药的统称,是反映中华民族对生命、健康和疾病的认识,具有悠久历史传统和独特理论及技术方法的医药学体系,是中华民族的瑰宝.某科研机构研究发现,某品种中医药的药物成分甲的含量![]() (单位:克)与药物功效
(单位:克)与药物功效![]() (单位:药物单位)之间具有关系
(单位:药物单位)之间具有关系![]() .检测这种药品一个批次的5个样本,得到成分甲的平均值为4克,标准差为
.检测这种药品一个批次的5个样本,得到成分甲的平均值为4克,标准差为![]() 克,则估计这批中医药的药物功效的平均值为( )
克,则估计这批中医药的药物功效的平均值为( )
A.22药物单位B.20药物单位C.12药物单位D.10药物单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若存在常数![]()
![]() ,使得数列
,使得数列![]() 满足
满足![]() 对一切
对一切![]() 恒成立,则称
恒成立,则称![]() 为可控数列,
为可控数列,![]() .
.
(1)若![]() ,
,![]() ,问
,问![]() 有多少种可能?
有多少种可能?
(2)若![]() 是递增数列,
是递增数列,![]() ,且对任意的
,且对任意的![]() ,数列
,数列![]() ,
,![]() ,
,![]()
![]() 成等差数列,判断
成等差数列,判断![]() 是否为可控数列?说明理由;
是否为可控数列?说明理由;
(3)设单调的可控数列![]() 的首项
的首项![]() ,前
,前![]() 项和为
项和为![]() ,即
,即![]() .问
.问![]() 的极限是否存在,若存在,求出
的极限是否存在,若存在,求出![]() 与
与![]() 的关系式;若不存在,请说明理由.
的关系式;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com