
分析 由m=-1,m<-1,-1<m<3,m=3,m>3,进行分类讨论,由此能求出关于x的不等式(m+1)x2-4x+1≤0(m∈R)的解集.
解答 解:∵(m+1)x2-4x+1≤0(m∈R),
(1)当m=-1时,原不等式为-4x+1≤0,解集为{x|x$≥\frac{1}{4}$},…(2分)
(2)当m<-1时,
解方程(m+1)x2-4x+1=0,得x=$\frac{4±\sqrt{16-4(m+1)}}{2(m+1)}$=$\frac{2±\sqrt{3-m}}{m+1}$,
原不等式的解集为{x|x≥$\frac{2-\sqrt{3-m}}{m+1}$或$x≤\frac{2+\sqrt{3-m}}{m+1}$}.…(5分)
(3)当-1<m<3时,
解方程(m+1)x2-4x+1=0,
得x=$\frac{4±\sqrt{16-4(m+1)}}{2(m+1)}$=$\frac{2±\sqrt{3-m}}{m+1}$,
原不等式的解集为{x|$\frac{2-\sqrt{3-m}}{m+1}$≤x≤$\frac{2+\sqrt{3-m}}{m+1}$},…(8分)
(4)当m=3时,原不等式为4x2-4x+1≤0,解集为{x|x=$\frac{1}{2}$},…(10分)
(5)当m>3时,方程(m+1)x2-4x+1=0无解,
原不等式的解集∅.…(12分)
点评 本题考查关于x的一元二次不等式的解法,是中档题,解题时要认真审题,注意分类讨论思想的合理运用.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≤-4 | B. | a≤-2 | C. | a≥-2 | D. | a>-4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 210 | B. | 245 | C. | 288 | D. | 2511 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为3的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为3的等腰三角形.
已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为3的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为3的等腰三角形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
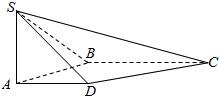 如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠ABC=90°,SA=AB=AD=1,BC=2.
如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠ABC=90°,SA=AB=AD=1,BC=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com