
【题目】如图,在四棱锥P-ABCD中,平面PCD⊥平面ABCD,![]() ,∠BAD=∠CDA=90°,
,∠BAD=∠CDA=90°,![]() .
.
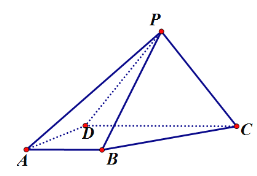
(1)求证:平面PAD⊥平面PBC;
(2)求直线PB与平面PAD所成的角;
(3)在棱PC上是否存在一点E使得直线![]() 平面PAD,若存在求PE的长,并证明你的结论.
平面PAD,若存在求PE的长,并证明你的结论.
【答案】(1)见解析; (2)![]() ; (3)存在
; (3)存在![]() 为
为![]() 中点,即
中点,即![]() 满足条件.
满足条件.
【解析】
(1)先证![]() 平面
平面![]() ;
;
(2)作出直线PB与平面PAD所成的角,再求出角的正切值,从而可得角;
(3)先假设存在,确定点的位置,再求出长度.
证明(1)因为∠BAD=∠CDA=90°,
所以![]() ,四边形
,四边形![]() 为直角梯形,
为直角梯形,![]()
又![]() 满足
满足![]()
![]()
又![]()
![]()
![]()
又![]() ,
,![]()
![]()
![]() ,
,![]()
所以平面PAD⊥平面PBC.
(2)取CD的中点H,连接BH,PH,作![]()
![]() 于
于![]() ,如图,
,如图,

在四边形ABCD中,![]() ,∠BAD=∠CDA=90°,
,∠BAD=∠CDA=90°,
所以![]() 为正方形,所以
为正方形,所以![]() ;
;
因为平面PCD⊥平面ABCD,平面PCD ![]() 平面ABCD=CD,所以
平面ABCD=CD,所以![]() 平面
平面![]() ;
;
所以![]() .
.
因为![]() ,所以
,所以![]() ;
;
在直角三角形![]() 中,
中,![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() 到平面
到平面![]() 的距离等于
的距离等于![]() ;
;
设直线PB与平面PAD所成的角为![]() ,则
,则![]() ,即直线PB与平面PAD所成的角为
,即直线PB与平面PAD所成的角为![]() .
.
(3)存在![]() 为
为![]() 中点,即
中点,即![]() 满足条件,证明如下:取
满足条件,证明如下:取![]() 中点
中点![]() ,连接
,连接![]() .如图,
.如图,
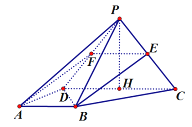
因为![]() 分别是
分别是![]() 的中点,所以
的中点,所以![]() 且
且![]() .
.
所以![]() 且
且![]() ,即
,即![]() 为平行四边形,所以
为平行四边形,所以![]() ;
;
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .此时
.此时![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在一次飞机航程中,调查男女晕机情况,在80名男乘客中有10人晕机,70人不晕机.在30名女乘客中有10人晕机,20人不晕机
(1)请根据题设数据列出![]() 列联表
列联表
晕机 | 不晕机 | 总计 | |
男 | |||
女 | |||
总计 |
(2)是否有![]() 把握认为“是否晕机与性别有关”.
把握认为“是否晕机与性别有关”.
附:![]()
| 0.050 | 0.025 | 0.010 |
| 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家电公司根据销售区域将销售员分成![]() 两组.2017年年初,公司根据销售员的销售业绩分发年终奖,销售员的销售额(单位:十万元)在区间
两组.2017年年初,公司根据销售员的销售业绩分发年终奖,销售员的销售额(单位:十万元)在区间![]() 内对应的年终奖分别为2万元,2.5万元,3万元,3.5万元.已知200名销售员的年销售额都在区间
内对应的年终奖分别为2万元,2.5万元,3万元,3.5万元.已知200名销售员的年销售额都在区间![]() 内,将这些数据分成4组:
内,将这些数据分成4组: ![]() ,得到如下两个频率分布直方图:
,得到如下两个频率分布直方图:

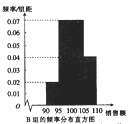
以上面数据的频率作为概率,分别从![]() 组与
组与![]() 组的销售员中随机选取1位,记
组的销售员中随机选取1位,记![]() 分别表示
分别表示![]() 组与
组与![]() 组被选取的销售员获得的年终奖.
组被选取的销售员获得的年终奖.
(1)求![]() 的分布列及数学期;
的分布列及数学期;
(2)试问![]() 组与
组与![]() 组哪个组销售员获得的年终奖的平均值更高?为什么?
组哪个组销售员获得的年终奖的平均值更高?为什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医院用光电比色计检查尿汞时,得尿汞含量(毫克/升)与消光系数如下表:
尿汞含量 | 2 | 4 | 6 | 8 | 10 |
消光系数 | 64 | 138 | 205 | 285 | 360 |
(1)作散点图;
(2)如果![]() 与
与![]() 之间具有线性相关关系,求回归线直线方程;
之间具有线性相关关系,求回归线直线方程;
(3)估计尿汞含量为9毫克/升时消光系数.
 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“微信”和“QQ”是腾讯社交体系中的两款产品,小明为了解不同群体对这两款产品的首选情况,统计了周围老师和同学关于首选“微信”或“QQ”的比例,得到如图等高条形图.根据等高条形图中的信息,可判断下列说法正确的是( )
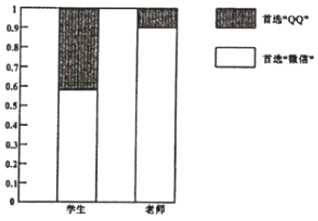
A.对老师而言,更倾向于首选“微信”
B.对学生而言,更倾向于首选“QQ”
C.首选“微信”的老师比首选“微信”的同学多
D.如果首选“微信”的老师比首选“微信”的同学多,则小明统计的老师人数一定比学生多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某摸球游戏的规则如下:从装有5个大小、形状完全相同的小球的盒中摸球(其中3个红球、2个黄球),每次摸一个球记录颜色并放回,若摸出红球记1分,摸出黄球记2分.
(1)求“摸球三次得分为5分”的概率;
(2)设ξ为摸球三次所得的分数,求随机变量ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解中学生课外阅读情况,现从某中学随机抽取![]() 名学生,收集了他们一年内的课外阅读量(单位:本)等数据,以下是根据数据绘制的统计图表的一部分.
名学生,收集了他们一年内的课外阅读量(单位:本)等数据,以下是根据数据绘制的统计图表的一部分.
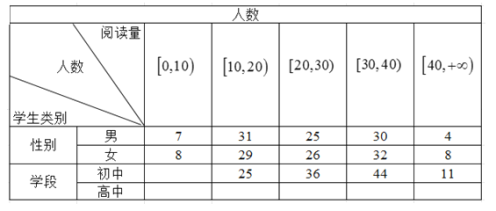
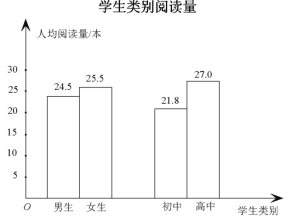
下面有四个推断:
①这![]() 名学生阅读量的平均数可能是
名学生阅读量的平均数可能是![]() 本;
本;
②这![]() 名学生阅读量的
名学生阅读量的![]() 分位数在区间
分位数在区间![]() 内;
内;
③这![]() 名学生中的初中生阅读量的中位数一定在区间
名学生中的初中生阅读量的中位数一定在区间![]() 内;
内;
④这![]() 名学生中的初中生阅读量的
名学生中的初中生阅读量的![]() 分位数可能在区间
分位数可能在区间![]() 内.
内.
所有合理推断的序号是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com