
【题目】如图,正四棱柱ABCD﹣A1B1C1D1中,AA1=2AB.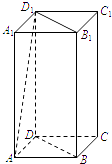
(1)求AD1与面BB1D1D所成角的正弦值;
(2)点E在侧棱AA1上,若二面角E﹣BD﹣C1的余弦值为 ![]() ,求
,求 ![]() 的值.
的值.
【答案】
(1)解:以D为原点,DA,DC,DD1分别为x轴,y轴,z轴,建立如图所示空间直角坐标系D﹣xyz.
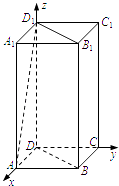
设AB=1,则D(0,0,0),A(1,0,0),
B(1,1,0),C(0,1,0),D1(0,0,2),
A1(1,0,2),B1(1,1,2),C1(0,1,2).
设AD1与面BB1D1D所成角的大小为θ, ![]() ,
,
设平面BB1D1D的法向量为 ![]() =(x,y,z),
=(x,y,z), ![]() ,
, ![]() ,
,
则 ![]() =0,
=0, ![]() ,即x+y=0,z=0.
,即x+y=0,z=0.
令x=1,则y=﹣1,所以n=(1,﹣1,0),
sinθ=|cos< ![]() >|=
>|= 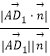 =
= ![]() ,
,
所以AD1与平面BB1D1D所成角的正弦值为 ![]()
(2)解:设E(1,0,λ),0≤λ≤2.
设平面EBD的法向量为 ![]() =(x1,y1,z1),平面BDC1的法向量为
=(x1,y1,z1),平面BDC1的法向量为 ![]() =(x2,y2,z2),
=(x2,y2,z2), ![]() ,
,
由 ![]() ,
, ![]() ,得x1+y1=0,x1+λz1=0,
,得x1+y1=0,x1+λz1=0,
令z1=1,则x1=﹣λ,y1=λ,n1=(﹣λ,λ,1), ![]() ,
,
由 ![]() ,
, ![]() ,得x2+y2=0,y2+2z2=0,
,得x2+y2=0,y2+2z2=0,
令z2=1,则x2=2,y2=﹣2,n2=(2,﹣2,1),
cos< ![]() >=
>= ![]() =
= ![]() ,
,
所以 ![]() ,得λ=1.
,得λ=1.
所以 ![]() =
= ![]() .
.
【解析】(1)建立空间直角坐标系,求出平面的法向量,利用向量法即可求AD1与面BB1D1D所成角的正弦值;(2)求出平面的法向量,根据二面角与平面法向量之间的关系进行求解即可.
【考点精析】掌握空间角的异面直线所成的角是解答本题的根本,需要知道已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则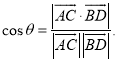 .
.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:
【题目】在棱长为2的正方体ABCD﹣A1B1C1D1中,E,F分别为AD,A1B1的中点.
(1)求证:DB1⊥CD1;
(2)求三棱锥B﹣EFC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+x2﹣xlna(a>0且a≠1)
(1)求函数f(x)单调递增区间;
(2)若存在x1 , x2∈[﹣1,1],使得|f(x1)﹣f(x2)|≥e﹣1(e是自然对数的底数),求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位N名员工参加“社区低碳你我他”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布图如图所示,下表是年龄的频率分布表.
,得到的频率分布图如图所示,下表是年龄的频率分布表.
![]()

(1)现要从年龄较小的第![]() 组中用分层抽样的方法抽取6人,则年龄第
组中用分层抽样的方法抽取6人,则年龄第![]() 组人数分别是多少?
组人数分别是多少?
(2)在(1)的条件下,从这6中随机抽取2参加社区宣传交流活动,X表示第3组中抽取的人数,求X的分布列和期望值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校有高级教师20人,中级教师30人,其他教师若干人,为了了解该校教师的工资收入情况,拟按分层抽样的方法从该校所有的教师中抽取20人进行调查.已知从其他教师中共抽取了10人,则该校共有教师人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com