
【题目】已知二次函数f(x)=x2-(2m+1)x+m.
(1)若方程f(x)=0有两个不等的实根x1,x2,且-1<x1<0<x2<1,求m的取值范围;
(2)若对任意的x∈[1,2],![]() ≤2恒成立,求m的取值范围.
≤2恒成立,求m的取值范围.
【答案】(1)(-![]() ,0) (2)[-
,0) (2)[-![]() ,+∞)
,+∞)
【解析】
(1)二次函数f(x)=x2-(2m+1)x+m开口向上,方程f(x)=0有两个不等的实根x1,x2,且-1<x1<0<x2<1,找到等价条件,解不等式组即可;
(2)把对任意的x∈[1,2],![]() ≤2恒成立,等价转换为对任意的x∈[1,2],x2-(2m+3)x+m≤0恒成立,得到关于m的不等式组
≤2恒成立,等价转换为对任意的x∈[1,2],x2-(2m+3)x+m≤0恒成立,得到关于m的不等式组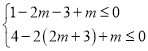 ,求解即可求得m的取值范围.
,求解即可求得m的取值范围.
(1)由方程f(x)=0有两个不等的实根x1,x2,且-1<x1<0<x2<1,
则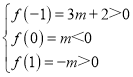 ,解得-
,解得-![]() <m<0,
<m<0,
∴m的取值范围是(-![]() ,0);
,0);
(2)对任意的x∈[1,2],![]() ≤2恒成立,即对任意的x∈[1,2],x2-(2m+1)x+m≤2x恒成立,
≤2恒成立,即对任意的x∈[1,2],x2-(2m+1)x+m≤2x恒成立,
∴对任意的x∈[1,2],x2-(2m+3)x+m≤0恒成立,
则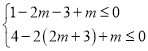 ,解得m≥-
,解得m≥-![]() ,
,
∴m的取值范围是[-![]() ,+∞).
,+∞).


科目:高中数学 来源: 题型:
【题目】已知m∈R,命题p:对任意x∈[0,1],不等式x2﹣2x﹣1≥m2﹣3m恒成立,命题q:存在x∈[﹣1,1],使得m≤2x﹣1;
(Ⅰ)若命题p为真命题,求m的取值范围;
(Ⅱ)若命題q为假命题,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医疗器械公司在全国共有![]() 个销售点,总公司每年会根据每个销售点的年销量进行评价分析.规定每个销售点的年销售任务为一万四千台器械.根据这
个销售点,总公司每年会根据每个销售点的年销量进行评价分析.规定每个销售点的年销售任务为一万四千台器械.根据这![]() 个销售点的年销量绘制出如下的频率分布直方图.
个销售点的年销量绘制出如下的频率分布直方图.
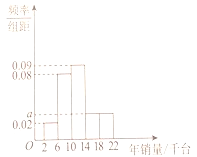
(1)完成年销售任务的销售点有多少个?
(2)若用分层抽样的方法从这![]() 个销售点中抽取容量为
个销售点中抽取容量为![]() 的样本,求该五组
的样本,求该五组![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,(单位:千台)中每组分别应抽取的销售点数量.
,(单位:千台)中每组分别应抽取的销售点数量.
(3)在(2)的条件下,从该样本中完成年销售任务的销售点中随机选取![]() 个,求这两个销售点不在同一组的概率.
个,求这两个销售点不在同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() .以坐标原点为极点,以
.以坐标原点为极点,以![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() .若点
.若点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 经过点
经过点![]() 且与曲线
且与曲线![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() ,
,![]() 两点间的距离
两点间的距离![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调查中国及美国的高中生在“家”、“朋友聚集的地方”、“个人空间”这三个场所中感到最幸福的场所是哪个,从中国某城市的高中生中随机抽取了55人,从美国某城市高中生中随机抽取了45人进行答题。中国高中生的答题情况:选择“家”的高中生的人数占![]() ,选择“朋友聚集的地方”的高中生的人数占
,选择“朋友聚集的地方”的高中生的人数占![]() ,选择“个人空间”的高中生的人数占
,选择“个人空间”的高中生的人数占![]() ,美国高中生的答题情况:选择“家”的高中生的人数占
,美国高中生的答题情况:选择“家”的高中生的人数占![]() ,选择“朋友聚集的地方”的高中生的人数占
,选择“朋友聚集的地方”的高中生的人数占![]() ,选择“个人空间”的高中生的人数占
,选择“个人空间”的高中生的人数占![]() 。
。
(1)请根据以上调查结果将下面的2X2列联表补充完整,并判断能否有95%的把握认为恋家(在家里感到最幸福)与国别有关;
在家里感到最幸福 | 在其他场所感到最幸福 | 总计 | |
中国高中生 | |||
美国高中生 | |||
总计 |
(2)从被调查的不“恋家”的美国高中生中,用分层抽样的方法随机选出4人接受进一步调查,再从4人中随机选出2人到中国交流学习,求2人中含有在“个人空间”感到最幸福的高中生的概率。
| 0.050 | 0.025 | 0.010 | 0.001 |
| 3.841 | 5.024 | 6.635 | 10.8 |
附:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={x|x2-3x+2=0},B={x|x2+(a-1)x+a2-5=0}.
(1)若A∩B={2},求实数a的值;
(2)若A∪B=A,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)满足条件f(0)=1,及f(x+1)﹣f(x)=2x.
(1)求函数f(x)的解析式;
(2)在区间[﹣1,1]上,y=f(x)的图象恒在y=2x+m的图象上方,试确定实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲袋内摸出1个红球的概率是![]() ,从乙袋内摸出1个红球的概率是
,从乙袋内摸出1个红球的概率是![]() ,从两袋内各摸出1个球,则
,从两袋内各摸出1个球,则![]() 等于( )
等于( )
A. 2个球不都是红球的概率B. 2个球都是红球的概率
C. 至少有1个红球的概率D. 2个球中恰好有1个红球的概率
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com