
【题目】某人坚持跑步锻炼,根据他最近20周的跑步数据,制成如下条形图:
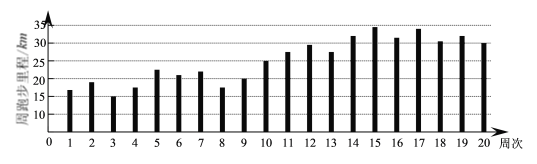
根据条形图判断,下列结论正确的是( )
A.周跑步里程逐渐增加
B.这20周跑步里程平均数大于30km
C.这20周跑步里程中位数大于30km
D.前10周的周跑步里程的极差大于后10周的周跑步里程的极差
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面ABCD为直角梯形,AB//CD,
中,底面ABCD为直角梯形,AB//CD,![]()
![]() 是以
是以![]() 为斜边的等腰直角三角形,且平面
为斜边的等腰直角三角形,且平面![]() 平面ABCD,点F满足,
平面ABCD,点F满足,![]() .
.
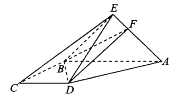
(1)试探究![]() 为何值时,CE//平面BDF,并给予证明;
为何值时,CE//平面BDF,并给予证明;
(2)在(1)的条件下,求直线AB与平面BDF所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以直角坐标系的原点
为参数).以直角坐标系的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立坐标系,曲线
轴的正半轴为极轴建立坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)若过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,与
两点,与![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
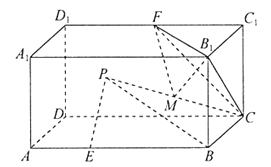
【题目】古希腊数学家阿波罗尼奥斯发现:平面上到两定点![]() ,
,![]() 距离之比为常数
距离之比为常数![]() 且
且![]() 的点的轨迹是一个圆心在直线
的点的轨迹是一个圆心在直线![]() 上的圆,该圆简称为阿氏圆.根据以上信息,解决下面的问题:如图,在长方体
上的圆,该圆简称为阿氏圆.根据以上信息,解决下面的问题:如图,在长方体![]() 中,
中,![]() ,点
,点![]() 在棱
在棱![]() 上,
上,![]() ,动点
,动点![]() 满足
满足![]() .若点
.若点![]() 在平面
在平面![]() 内运动,则点
内运动,则点![]() 所形成的阿氏圆的半径为________;若点
所形成的阿氏圆的半径为________;若点![]() 在长方体
在长方体![]() 内部运动,
内部运动,![]() 为棱
为棱![]() 的中点,
的中点,![]() 为
为![]() 的中点,则三棱锥
的中点,则三棱锥![]() 的体积的最小值为___________.
的体积的最小值为___________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 满足
满足![]() ,
,![]() ,记数列
,记数列![]() 的前n项和是
的前n项和是![]() ,则( )
,则( )
A.若数列![]() 是常数列,则
是常数列,则![]()
B.若![]() ,则数列
,则数列![]() 单调递减
单调递减
C.若![]() ,则
,则![]()
D.若![]() ,任取
,任取![]() 中的9项
中的9项![]() 构成数列
构成数列![]() 的子数列
的子数列![]() ,则
,则![]() 不全是单调数列
不全是单调数列
查看答案和解析>>
科目:高中数学 来源: 题型:
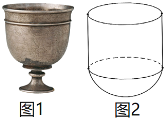
【题目】唐朝的狩猎景象浮雕银杯如图1所示.其浮雕临摹了国画、漆绘和墓室壁画,体现了古人的智慧与工艺.它的盛酒部分可以近似地看作是半球与圆柱的组合体(假设内壁表面光滑,忽略杯壁厚度),如图2所示.已知球的半径为R,酒杯内壁表面积为![]() ,设酒杯上部分(圆柱)的体积为
,设酒杯上部分(圆柱)的体积为![]() ,下部分(半球)的体积为
,下部分(半球)的体积为![]() ,则
,则![]() ( )
( )
A.2B.![]() C.1D.
C.1D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() 为边
为边![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 翻转成
翻转成![]() (
(![]() 平面
平面![]() ).若
).若![]() 分别为线段
分别为线段![]() 的中点,则在
的中点,则在![]() 翻转过程中,下列说法正确的是( )
翻转过程中,下列说法正确的是( )
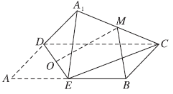
A.与平面![]() 垂直的直线必与直线
垂直的直线必与直线![]() 垂直
垂直
B.异面直线![]() 与
与![]() 所成的角是定值
所成的角是定值
C.一定存在某个位置,使![]()
D.三棱锥![]() 外接球半径与棱
外接球半径与棱![]() 的长之比为定值
的长之比为定值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com