
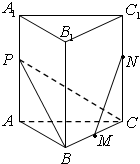
 ��ͼ������������ABC-A1B1C1�У�������ij��ȶ���1��M��BC�ߵ��е㣬P��AA1���ϵĵ㣬��PA=
��ͼ������������ABC-A1B1C1�У�������ij��ȶ���1��M��BC�ߵ��е㣬P��AA1���ϵĵ㣬��PA=
| ||
| 4 |
| BP |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 4 |
| BC |
| ||
| 2 |
| 1 |
| 2 |
| NM |
| ||
| 4 |
| 3 |
| 4 |
| AB1 |
| ||
| 2 |
| 1 |
| 2 |
| ||||||
|
| 1 |
| 8 |
| ||
| 4 |
| ||
| 2 |
| 1 |
| 2 |
|
| 3 |
| 2 |
| 3 |
| x |
| 1 |
| y | ||
|
| z | ||
2
|
| x |
| 1 |
| y | ||
|
| z | ||
2
|
| ||
| 12 |
| 1 |
| 4 |
| ||
| 6 |
| ||
| 6 |
| 1 |
| 2 |
| ||
| 3 |
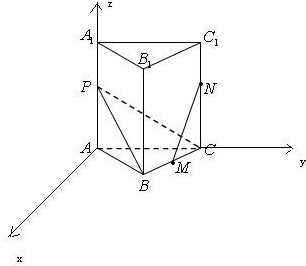 �⣺��1����AΪԭ�㣬��AB˳ʱ����ת30��õ���ֱ��Ϊx�ᣬ
�⣺��1����AΪԭ�㣬��AB˳ʱ����ת30��õ���ֱ��Ϊx�ᣬ
| ||
| 4 |
| ||
| 4 |
| ||
| 2 |
| 1 |
| 2 |
| BP |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 4 |
| BC |
| ||
| 2 |
| 1 |
| 2 |
| BP |
1-(cos��
|
| ||
| 4 |
1-(
|
3
| ||
| 4 |
| ||
| 4 |
| 3 |
| 4 |
| ||
| 2 |
| 1 |
| 2 |
| NM |
| ||
| 4 |
| 3 |
| 4 |
| AB1 |
| ||
| 2 |
| 1 |
| 2 |
| ||||||
|
| ||||
|
| 1 |
| 8 |
| ||
| 4 |
| ||
| 2 |
| 1 |
| 2 |
|
2
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
2
| ||
| 3 |
| 3 |
| 2 |
| 3 |
| x |
| 1 |
| y | ||
|
| z | ||
2
|
| x |
| 1 |
| y | ||
|
| z | ||
2
|
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| ||
| 12 |
| ||
| 12 |
| 1 |
| 4 |
| ||
| 6 |
| ||
| 12 |
| ||
| 6 |
| 1 |
| 4 |
| 1 |
| 2 |
���ϰ��
��Ŀ��������ѧ ��Դ�� ���ͣ�  ��ͼ������������ABC-A1B1C1�У�AB=1���������C-AB-C1�Ĵ�СΪ60�㣬���C��ƽ��C1AB�ľ���Ϊ�������� ��ͼ������������ABC-A1B1C1�У�AB=1���������C-AB-C1�Ĵ�СΪ60�㣬���C��ƽ��C1AB�ľ���Ϊ��������
�鿴�𰸺ͽ���>> ��Ŀ��������ѧ ��Դ�� ���ͣ� ��ͼ������������ABC-A1B1C1�У���֪AB=1��D����BB1�ϣ���BD=1����AD��ƽ��AA1CC1���ɵĽ�Ϊa����sina= �鿴�𰸺ͽ���>> ��Ŀ��������ѧ ��Դ�� ���ͣ�  ��ͼ������������ABC-A1B1C1�У�D��E��G�ֱ���AB��BB1��AC1���е㣬AB=BB1=2�� ��ͼ������������ABC-A1B1C1�У�D��E��G�ֱ���AB��BB1��AC1���е㣬AB=BB1=2����������B1C1���Ƿ���ڵ�FʹGF��DE��������ڣ���ȷ������λ�ã���������ڣ���˵�����ɣ� ���������DEG�����ABC���������ǵ�����ֵ�� ������B1������DEG�ľ��룮 �鿴�𰸺ͽ���>> ��Ŀ��������ѧ ��Դ�� ���ͣ�  ��ͼ������������ABC-A1B1C1�У�AA1=4��AB=2��M��AC���е㣬��N��AA1�ϣ�AN= ��ͼ������������ABC-A1B1C1�У�AA1=4��AB=2��M��AC���е㣬��N��AA1�ϣ�AN=
������BC1�����ACC1A1���ɽǵĴ�С�� ����������C1-BM-C������ֵ�� ����֤��MN��BC1�� �鿴�𰸺ͽ���>> ��Ŀ��������ѧ ��Դ�� ���ͣ�  ��2012•����ɽ��ģ����ͼ������������ABCһDEF�У�AB=2��AD=1��P��CF���ӳ�����һ�㣬��A��B��P�����ƽ�潻FD��M����EF��N�� ��2012•����ɽ��ģ����ͼ������������ABCһDEF�У�AB=2��AD=1��P��CF���ӳ�����һ�㣬��A��B��P�����ƽ�潻FD��M����EF��N����I����֤��MN��ƽ��CDE�� ��II����ƽ��PAB��ƽ��CDEʱ��������̨MNF-ABC������� �鿴�𰸺ͽ���>> ͬ����ϰ��� ����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר�� Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com��Ȩ��������վ�������£�ͼƬ��Դ�����磬����Ȩ����Ȩ��ԭ�������У�ת�������ַ���Ȩ��������Ȩ����������������֪�����ǽ����촦������ϵqq��3310059649�� ICP�������: ��ICP��07509807��-10 ����������42018502000812�� | |||||||||||||||||||||||||||||||||||