
【题目】已知函数f(x)= ![]() 若存在实数b,使函数g(x)=f(x)﹣b有两个零点,则a的取值范围是 .
若存在实数b,使函数g(x)=f(x)﹣b有两个零点,则a的取值范围是 .
【答案】{a|a<0或a>1}
【解析】解:∵g(x)=f(x)﹣b有两个零点,
∴f(x)=b有两个零点,即y=f(x)与y=b的图像有两个交点,
由x3=x2可得,x=0或x=1
①当a>1时,函数f(x)的图像如图所示,此时存在b,满足题意,故a>1满足题意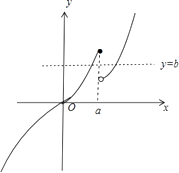
②当a=1时,由于函数f(x)在定义域R上单调递增,故不符合题意
③当0<a<1时,函数f(x)单调递增,故不符合题意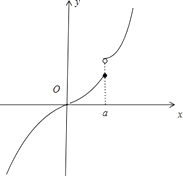
④a=0时,f(x)单调递增,故不符合题意
⑤当a<0时,函数y=f(x)的图像如图所示,此时存在b使得,y=f(x)与y=b有两个交点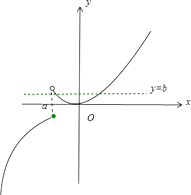
综上可得,a<0或a>1
所以答案是:{a|a<0或a>1}
【考点精析】本题主要考查了函数的零点的相关知识点,需要掌握函数的零点就是方程的实数根,亦即函数的图象与轴交点的横坐标.即:方程有实数根,函数的图象与坐标轴有交点,函数有零点才能正确解答此题.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ)(ω>0,|φ|< ![]() )的最小正周期是π,若将其图象向右平移
)的最小正周期是π,若将其图象向右平移 ![]() 个单位后得到的图象关于原点对称,则函数f(x)的图象( )
个单位后得到的图象关于原点对称,则函数f(x)的图象( )
A.关于直线x= ![]() 对称
对称
B.关于直线x= ![]() 对称
对称
C.关于点( ![]() ,0)对称
,0)对称
D.关于点( ![]() ,0)对称
,0)对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(x+ ![]() ﹣2)(a>0) (Ⅰ)当1<a<4时,函数f(x)在[2,4]上的最小值为ln
﹣2)(a>0) (Ⅰ)当1<a<4时,函数f(x)在[2,4]上的最小值为ln ![]() ,求a;
,求a;
(Ⅱ)若存在x0∈(2,+∞),使得f(x0)<0,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在半径为 ![]() ,圆心角为60°的扇形的弧上任取一点P,作扇形的内接矩形PNMQ,使点Q在OA上,点N,M在OB上,设矩形PNMQ的面积为y,∠POB=θ.
,圆心角为60°的扇形的弧上任取一点P,作扇形的内接矩形PNMQ,使点Q在OA上,点N,M在OB上,设矩形PNMQ的面积为y,∠POB=θ. 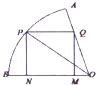
(1)将y表示成θ的函数关系式,并写出定义域;
(2)求矩形PNMQ的面积取得最大值时 ![]()
![]() 的值;
的值;
(3)求矩形PNMQ的面积y≥ ![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() =(sinx,cosx),
=(sinx,cosx), ![]() =(sinx,sinx),
=(sinx,sinx), ![]() =(﹣1,0)
=(﹣1,0)![]()
(1)若x= ![]() ,求
,求 ![]() 与
与 ![]() 的夹角θ;
的夹角θ;
(2)若x∈[﹣ ![]() ,
, ![]() ],f(x)=λ
],f(x)=λ ![]()
![]() 的最大值为
的最大值为 ![]() ,求λ.
,求λ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=mex﹣x﹣1(其中e为自然对数的底数,),若f(x)=0有两根x1 , x2且x1<x2 , 则函数y=(e ![]() ﹣e
﹣e ![]() )(
)( ![]() ﹣m)的值域为 .
﹣m)的值域为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①存在实数x,使sinx+cosx= ![]() ;
;
②若α,β是第一象限角,且α>β,则cosα<cosβ;
③函数y=sin( ![]() x+
x+ ![]() )是偶函数;
)是偶函数;
④函数y=sin2x的图象向左平移 ![]() 个单位,得到函数y=cos2x的图象.
个单位,得到函数y=cos2x的图象.
其中正确命题的序号是(把正确命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某海滨浴场每年夏季每天的海浪高度y(米)是时间x(0≤x≤24,单位:小时)的函数,记作y=f(x),下表是每年夏季每天某些时刻的浪高数据:
x(时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
y(米) | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 |
(1)经观察发现可以用三角函数y=Acosωx+b对这些数据进行拟合,求函数f(x)的表达式;
(2)浴场规定,每天白天当海浪高度高于1.25米时,才对冲浪爱好者开放,求冲浪者每天白天可以在哪个时段到该浴场进行冲浪运动?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知首项是1的两个数列{an},{bn}(bn≠0,n∈N*)满足anbn+1﹣an+1bn+2bn+1bn=0.
(1)令cn= ![]() ,求数列{cn}的通项公式;
,求数列{cn}的通项公式;
(2)若bn=3n﹣1 , 求数列{an}的前n项和Sn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com