
 在生产过程中,测得100件纤维产品的纤度(表示纤维粗细的一种量),将数据分组如表.
在生产过程中,测得100件纤维产品的纤度(表示纤维粗细的一种量),将数据分组如表.| 分组 | 频数 | 频率 |
| [1.30,1.34) | 4 | |
| [1.34,1.38) | 25 | |
| [1.38,1.42) | 30 | |
| [1.42,1.46) | 29 | |
| [1.46,1.50) | 10 | |
| [1.50,1.54) | 2 | |
| 合计 | 100 |
分析 (Ⅰ)由频率=$\frac{频数}{总数}$,根据已知条件能完成频率分布表,从而能画出频率分布直方图.
(Ⅱ)由已知得ξ的可能取值为0,1,2,分别求出相应的概率,由此能求出ξ的分布列和Eξ.
解答 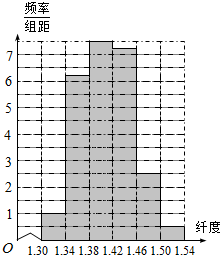 解:(Ⅰ)由频率=$\frac{频数}{总数}$,完成频率分布表如下:
解:(Ⅰ)由频率=$\frac{频数}{总数}$,完成频率分布表如下:
| 分组 | 频数 | 频率 |
| [1.30,1.34) | 4 | 0.04 |
| [1.34,1.38) | 25 | 0.25 |
| [1.38,1.42) | 30 | 0.30 |
| [1.42,1.46) | 29 | 0.29 |
| [1.46,1.50) | 10 | 0.10 |
| [1.50,1.54) | 2 | 0.02 |
| 合计 | 100 | 1.00 |
| ξ | 0 | 1 | 2 |
| P | $\frac{1}{15}$ | $\frac{8}{15}$ | $\frac{6}{15}$ |
点评 本题考查频率分布表和频率分布直方图的作法,考查离散型随机变量的分布列和期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源:2016-2017学年安徽豪州蒙城县一中高二上月考一数学试卷(解析版) 题型:解答题
已知等比数列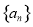 ,各项
,各项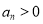 ,公比为
,公比为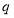 .(1)设
.(1)设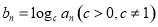 ,求证:
,求证:
(1)数列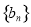 是等差数列,并求出该数列的首项
是等差数列,并求出该数列的首项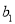 及公差
及公差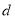 ;
;
(2)设(1)中的数列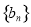 单调递减,求公比
单调递减,求公比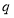 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 从某体校学生中选出男生14人,女生6人测量身高,被测学生身高的茎叶图如图所示(单位:cm),现规定,身高在180cm以上的参加校篮球队,180cm以下的参加田径队.
从某体校学生中选出男生14人,女生6人测量身高,被测学生身高的茎叶图如图所示(单位:cm),现规定,身高在180cm以上的参加校篮球队,180cm以下的参加田径队.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$<a<$\frac{3}{2}$ | B. | $\frac{1}{2}$≤a≤$\frac{3}{2}$ | C. | a<$\frac{1}{2}$或a>$\frac{3}{2}$ | D. | a≤$\frac{1}{2}$或a≥$\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f($\frac{π}{6}$)>$\sqrt{3}$f($\frac{π}{3}$) | B. | f($\frac{π}{6}$)<$\sqrt{3}$f($\frac{π}{3}$) | C. | $\sqrt{3}$f($\frac{π}{6}$)>f($\frac{π}{3}$) | D. | $\sqrt{3}$f($\frac{π}{6}$)<f($\frac{π}{3}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com