
【题目】设函数 ![]() ,
,
(1)求证: ![]() ;
;
(2)当x≥1时,f(x)≥lnx﹣a(x﹣1)恒成立,求a的取值范围.
【答案】
(1)证明:要证明 ![]() ,即
,即 ![]() ,
,
∵x>0,∴也就是要证明lnx≤x﹣1,即lnx﹣x+1≤0,
下面证明lnx﹣x+1≤0恒成立,
令g(x)=lnx﹣x+1, ![]() ,令g'(x)=0,得x=1,
,令g'(x)=0,得x=1,
可知:g(x)在(0,1)上递增,在(1,+∞)上递减,
∴g(x)≤g(1)=ln1﹣1+1=0,
则 ![]() ;
;
(2)解:当x≥1时,f(x)≥lnx﹣a(x﹣1)恒成立, ![]() ,即xlnx﹣a(x2﹣1)≤0,
,即xlnx﹣a(x2﹣1)≤0,
令h(x)=xlnx﹣a(x2﹣1),(x≥1),h'(x)=lnx+1﹣2ax,
令H(x)=lnx+1﹣2ax,∴ ![]() ,
,
①当a≤0时,H'(x)>0恒成立,
∴H(x)在[1,+∞)上递增,h'(x)=H(x)≥H(1)=1﹣2a>0,
∴h(x)在[1,+∞)上递增,
∴h(x)≥h(1)=0,
∴a≤0不符合题意;
②当 ![]() 时,
时, ![]() ,
,
当 ![]() 时,H'(x)>0,H(x)递增,h'(x)=H(x)≥H(1)=1﹣2a>0,
时,H'(x)>0,H(x)递增,h'(x)=H(x)≥H(1)=1﹣2a>0,
从而h(x)在 ![]() 上递增,
上递增,
∴h(x)≥h(1)=0,
∴ ![]() 不符合题意;
不符合题意;
③当 ![]() 时,
时, ![]() ,H'(x)<0恒成立,
,H'(x)<0恒成立,
∴H(x)在[1,+∞)上递减,h'(x)=H(x)≤H(1)=1﹣2a<0,
∴h(x)在[1,+∞)上递减,
∴h(x)≤h(1)=0,
∴ ![]() 符合题意.
符合题意.
综上所述:a的取值范围是 ![]() .
.
【解析】(1)要证明 f ( x ) ≤ 1 ![]() ,只需要证明lnx≤x﹣1,构造函数g(x)=lnx﹣x+1,通过求导不难证明g(x)≤g(1)=0,结论得证;(2)当x≥1时,f(x)≥lnx﹣a(x﹣1)恒成立,即xlnx﹣a(x2﹣1)≤0,构造函数h(x)=xlnx﹣a(x2﹣1),通过求导后分情况讨论①a≤0时,②0 < a <
,只需要证明lnx≤x﹣1,构造函数g(x)=lnx﹣x+1,通过求导不难证明g(x)≤g(1)=0,结论得证;(2)当x≥1时,f(x)≥lnx﹣a(x﹣1)恒成立,即xlnx﹣a(x2﹣1)≤0,构造函数h(x)=xlnx﹣a(x2﹣1),通过求导后分情况讨论①a≤0时,②0 < a < ![]() ,③a≥
,③a≥![]() 三个情况可得出a的取值范围.
三个情况可得出a的取值范围.


科目:高中数学 来源: 题型:
【题目】小张于年初支出50万元购买一辆大货车,第一年因缴纳各种费用需支出6万元,从第二年起,每年都比上一年增加支出2万元,假定该车每年的运输收入均为25万元.小张在该车运输累计收入超过总支出后,考虑将大货车作为二手车出售,若该车在第x年年底出售,其销售收入为25﹣x万元(国家规定大货车的报废年限为10年).
(1)大货车运输到第几年年底,该车运输累计收入超过总支出?
(2)在第几年年底将大货车出售,能使小张获得的年平均利润最大?(利润=累计收入+销售收入﹣总支出)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=nx﹣xn , x∈R,其中n∈N , 且n≥2.
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)设曲线y=f(x)与x轴正半轴的交点为P,曲线在点P处的切线方程为y=g(x),求证:对于任意的正实数x,都有f(x)≤g(x);
(Ⅲ)若关于x的方程f(x)=a(a为实数)有两个正实数根x1 , x2 , 求证:|x2﹣x1|< ![]() +2.
+2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市随机抽取部分企业调查年上缴税收情况{单位万元,将所得数据绘制成频率分布直方图(如图),年上缴税收范围是[0,100]样本数据分组为[0,20),[20,40)[40,60)[60,80),[80,100)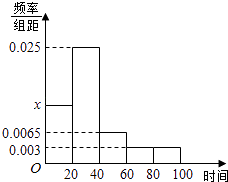
(1)求直方图中x的值;
(2)如果年上缴税收不少于60万元的企业可申请政策优惠,若共抽取企业1200个,试估计有多少企业可以申请政策优惠;
(3)从企业中任选4个,这4个企业年上缴税收少于20万元的个数记为X,求X的分布列和数学期望(以直方图中的频率作为概率)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 存在互不相等实数a,b,c,d,有f(a)=f(b)=f(c)=f(d)=m.现给出三个结论:
存在互不相等实数a,b,c,d,有f(a)=f(b)=f(c)=f(d)=m.现给出三个结论:
⑴m∈[1,2);
⑵a+b+c+d∈[e﹣3+e﹣1﹣2,e﹣4﹣1),其中e为自然对数的底数;
⑶关于x的方程f(x)=x+m恰有三个不等实根.
正确结论的个数为( )
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水.天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸.若盆中积水深九寸,则平地降雨量是( )
(注:①平地降雨量等于盆中积水体积除以盆口面积;②一尺等于十寸;③台体的体积公式V= ![]() )
)
A.2寸
B.3寸
C.4寸
D.5寸
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】广东佛山某学校参加暑假社会实践活动知识竞赛的学生中,得分在[80,90)中的有16人,得分在[90,100]中的有4人,用分层抽样的方法从得分在[80,100]的学生中抽取一个容量为5的样本,将该样本看成一个整体,从中任意选取2人,则其中恰有1人分数不低于90的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设定义在(0,+∞)上的单调函数f(x),对任意的x∈(0,+∞)都有f[f(x)﹣log2x]=3,若方程f(x)+f′(x)=a有两个不同的实数根,则实数a的取值范围是( )
A.(1,+∞)
B.(2+ ![]() ,+∞)
,+∞)
C.(2﹣ ![]() ,+∞)
,+∞)
D.(3,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com