
【题目】设函数f′(x)是奇函数f(x)(x∈R)的导函数,f(﹣1)=0,当x>0时,xf′(x)﹣f(x)<0,则使得f(x)>0成立的x的取值范围是( )
A.(﹣∞,﹣1)∪(0,1)
B.(﹣1,0)∪(1,+∞)
C.(﹣∞,﹣1)∪(﹣1,0)
D.(0,1)∪(1,+∞)
【答案】A
【解析】解:设g(x)= ![]() ,则g(x)的导数为:g′(x)=
,则g(x)的导数为:g′(x)= ![]() , ∵当x>0时总有xf′(x)<f(x)成立,
, ∵当x>0时总有xf′(x)<f(x)成立,
即当x>0时,g′(x)恒小于0,
∴当x>0时,函数g(x)= ![]() 为减函数,
为减函数,
又∵g(﹣x)= ![]() =
= ![]() =
= ![]() =g(x),
=g(x),
∴函数g(x)为定义域上的偶函数
又∵g(﹣1)= ![]() =0,
=0,
∴函数g(x)的图象性质类似如图:
数形结合可得,不等式f(x)>0xg(x)>0
![]() 或
或 ![]() ,
,
0<x<1或x<﹣1.
故选:A.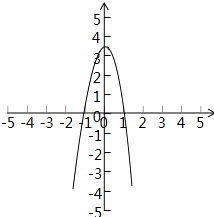
由已知当x>0时总有xf′(x)﹣f(x)<0成立,可判断函数g(x)= ![]() 为减函数,由已知f(x)是定义在R上的奇函数,可证明g(x)为(﹣∞,0)∪(0,+∞)上的偶函数,根据函数g(x)在(0,+∞)上的单调性和奇偶性,模拟g(x)的图象,而不等式f(x)>0等价于xg(x)>0,数形结合解不等式组即可.
为减函数,由已知f(x)是定义在R上的奇函数,可证明g(x)为(﹣∞,0)∪(0,+∞)上的偶函数,根据函数g(x)在(0,+∞)上的单调性和奇偶性,模拟g(x)的图象,而不等式f(x)>0等价于xg(x)>0,数形结合解不等式组即可.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知f(x)= ![]()
![]() ,其中
,其中 ![]() =(2cosx,﹣
=(2cosx,﹣ ![]() sin2x),
sin2x), ![]() =(cosx,1)(x∈R).
=(cosx,1)(x∈R).
(1)求f(x)的周期和单调递减区间;
(2)在△ABC 中,角A、B、C的对边分别为a,b,c,f(A)=﹣1,a= ![]() ,
, ![]()
![]() =3,求边长b和c的值(b>c).
=3,求边长b和c的值(b>c).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】log0.72,log0.70.8,0.9﹣2的大小顺序是( )
A.log0.72<log0.70.8<0.9﹣2
B.log0.70.8<log0.72<0.9﹣2
C.0.9﹣2<log0.72<log0.70.8
D.log0.72<0.9﹣2<log0.70.8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙、丁四人进行选择题解题比赛,已知每个选择题选择正确得![]() 分,否则得
分,否则得![]() 分.其测试结果如下:甲解题正确的个数小于乙解题正确的个数,乙解题正确的个数小于丙解题正确的个数,丙解题正确的个数小于丁解题正确的个数;且丁解题正确的个数的
分.其测试结果如下:甲解题正确的个数小于乙解题正确的个数,乙解题正确的个数小于丙解题正确的个数,丙解题正确的个数小于丁解题正确的个数;且丁解题正确的个数的![]() 倍小于甲解题正确的个数的
倍小于甲解题正确的个数的![]() 倍,则这四人测试总得分数最少为( )
倍,则这四人测试总得分数最少为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(n)=1+ ![]() +
+ ![]() +…+
+…+ ![]() (n∈N*),计算得f(2)=
(n∈N*),计算得f(2)= ![]() ,f(4)>2,f(8)>
,f(4)>2,f(8)> ![]() ,f(16)>3,f(32)>
,f(16)>3,f(32)> ![]() ,由此推算:当n≥2时,有( )
,由此推算:当n≥2时,有( )
A.f(2n)> ![]() (n∈N*)
(n∈N*)
B.f(2n)> ![]() (n∈N*)
(n∈N*)
C.f(2n)> ![]() (n∈N*)
(n∈N*)
D.f(2n)> ![]() (n∈N*)
(n∈N*)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小王在某景区内销售该景区纪念册,纪念册每本进价为5元,每销售一本纪念册需向该景区管理部门交费2元,预计这种纪念册以每本20元的价格销售时,小王一年可销售2000本,经过市场调研发现,每本纪念册的销售价格在每本20元的基础上每减少一元则增加销售400本,而每增加一元则减少销售100本,现设每本纪念册的销售价格为x元.
![]() 写出小王一年内销售这种纪念册所获得的利润
写出小王一年内销售这种纪念册所获得的利润![]() 元
元![]() 与每本纪念册的销售价格
与每本纪念册的销售价格![]() 元
元![]() 的函数关系式,并写出这个函数的定义域;
的函数关系式,并写出这个函数的定义域;
![]() 当每本纪念册销售价格x为多少元时,小王一年内利润
当每本纪念册销售价格x为多少元时,小王一年内利润![]() 元
元![]() 最大,并求出这个最大值.
最大,并求出这个最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,圆C的方程为(x+6)2+y2=25. (Ⅰ)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求C的极坐标方程;
(Ⅱ)直线l的参数方程是 ![]() (t为参数),l与C交与A,B两点,|AB|=
(t为参数),l与C交与A,B两点,|AB|= ![]() ,求l的斜率.
,求l的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司共有职工1500人,其中男职工1050人,女职工450人.为调查该公司职工每周平均上网的时间,采用分层抽样的方法,收集了300名职工每周平均上网时间的样本数据(单位:小时)

男职工 | 女职工 | 总计 | |
每周平均上网时间不超过4个小时 | |||
每周平均上网时间超过4个小时 | 70 | ||
总计 | 300 |
(Ⅰ)应收集多少名女职工样本数据?
(Ⅱ)根据这300个样本数据,得到职工每周平均上网时间的频率分布直方图(如图所示),其中样本数据分组区间为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .试估计该公司职工每周平均上网时间超过4小时的概率是多少?
.试估计该公司职工每周平均上网时间超过4小时的概率是多少?
(Ⅲ)在样本数据中,有70名女职工的每周平均上网时间超过4个小时.请将每周平均上网时间与性别的![]() 列联表补充完整,并判断是否有95%的把握认为“该公司职工的每周平均上网时间与性别有关”
列联表补充完整,并判断是否有95%的把握认为“该公司职工的每周平均上网时间与性别有关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】身体素质拓展训练中,人从竖直墙壁的顶点A沿光滑杆自由下滑到倾斜的木板上(人可看作质点),若木板的倾斜角不同,人沿着三条不同路径AB、AC、AD滑到木板上的时间分别为t1、t2、t3,若已知AB、AC、AD与板的夹角分别为70o、90o和105o,则( )

A. t1>t2>t3 B. t1<t2<t3 C. t1=t2=t3 D. 不能确定t1、t2、t3之间的关系
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com