
某公司生产产品A,产品质量按测试指标分为:指标大于或等于90为一等品,大于或等于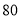 小于
小于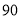 为二等品,小于
为二等品,小于 为三等品,生产一件一等品可盈利50元,生产一件二等品可盈利
为三等品,生产一件一等品可盈利50元,生产一件二等品可盈利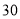 元,生产一件三等品亏损10元.现随机抽查熟练工人甲和新工人乙生产的这种产品各100件进行检测,检测结果统计如下:
元,生产一件三等品亏损10元.现随机抽查熟练工人甲和新工人乙生产的这种产品各100件进行检测,检测结果统计如下:
测试指标 |
|
|
|
|
|
|
甲 | 3 | 7 | 20 | 40 | 20 | 10 |
乙 | 5 | 15 | 35 | 35 | 7 | 3 |
根据上表统计得到甲、乙两人生产产品A为一等品、二等品、三等品的频率分别估计为他们生产产品A为一等品、二等品、三等品的概率.
(1)计算甲生产一件产品A,给工厂带来盈利不小于30元的概率;
(2)若甲一天能生产20件产品A,乙一天能生产15件产品A,估计甲乙两人一天生产的35件产品A中三等品的件数.
(1)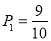 ;(2)参考解析
;(2)参考解析
【解析】
试题分析:(1)由题意可得100件产品中甲有10件指标小于80,所以给工厂带来盈利小于30元的概率为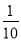 .所以甲生产一件产品A,给工厂带来盈利不小于30元的概率为
.所以甲生产一件产品A,给工厂带来盈利不小于30元的概率为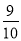 .
.
(2)依题意可得甲、乙生产一件产品A是三等品的件数分别为10,20.所以三等品的概率分别是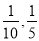 .所以甲一天能生产20件产品A,乙一天能生产15件产品A中的三等品件数为2,3.即可得甲乙两人一天生产的35件产品A中三等品的件数.
.所以甲一天能生产20件产品A,乙一天能生产15件产品A中的三等品件数为2,3.即可得甲乙两人一天生产的35件产品A中三等品的件数.
试题解析:(1)甲生产一件产品A,给工厂带来盈利不小于30元的概率为:
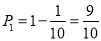 6分
6分
(2)估计甲一天生产的20件产品A中有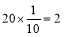 件三等品, 8分
件三等品, 8分
估计乙一天生产的15件产品A中有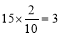 件三等品, 10分
件三等品, 10分
所以估计甲乙两人一天生产的35件产品A中共有5件三等品. 12分
考点:1.统计问题.2.根据频率估计概率.3.正难则反的解题思想.


科目:高中数学 来源:2013-2014学年江西省宜春市高三考前模拟理科数学试卷(解析版) 题型:解答题
已知函数g(x)=aln x·f(x)=x3 +x2+bx
(1)若f(x)在区间[1,2]上不是单调函数,求实数b的范围;
(2)若对任意x∈[1,e],都有g(x)≥-x2+(a+2)x恒成立,求实数a的取值范围;
(3)当b=0时,设F(x)= ,对任意给定的正实数a,曲线y=F(x)上是否存在两点P,Q,使得△POQ是以O(O为坐标原点)为直角顶点的直角三角形,而且此三角形斜边中点在y轴上?请说明理由.
,对任意给定的正实数a,曲线y=F(x)上是否存在两点P,Q,使得△POQ是以O(O为坐标原点)为直角顶点的直角三角形,而且此三角形斜边中点在y轴上?请说明理由.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省宜春市高三考前模拟文科数学试卷(解析版) 题型:选择题
已知全集为R,集合M ={xlx2-2x-8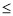 0),集合N={x|l-x<0},则集合M
0),集合N={x|l-x<0},则集合M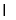 (CRN)等于( )
(CRN)等于( )
A.[-2,1] B.(1,+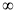 ) C.[-l,4) D.(1,4]
) C.[-l,4) D.(1,4]
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省南昌市高三第二次模拟考试理科数学试卷(解析版) 题型:选择题
已知函数 是周期为2的周期函数,且当
是周期为2的周期函数,且当 时,
时, ,则函数
,则函数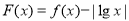 的零点个数是( )
的零点个数是( )
A.9 B.10 C.11 D.18

查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省南昌市高三第二次模拟考试文科数学试卷(解析版) 题型:解答题
已知函数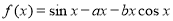
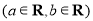 .
.
(1)若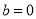 ,讨论函数
,讨论函数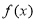 在区间
在区间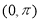 上的单调性;
上的单调性;
(2)若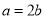 且
且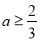 ,对任意的
,对任意的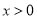 ,试比较
,试比较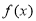 与
与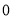 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省南昌市高三第二次模拟考试文科数学试卷(解析版) 题型:选择题
已知函数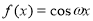
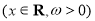 的最小正周期为
的最小正周期为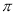 ,为了得到函数
,为了得到函数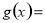
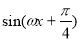 的图象,只要将
的图象,只要将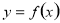 的图象( )
的图象( )
A.向左平移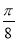 个单位长度 B.向右平移
个单位长度 B.向右平移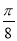 个单位长度
个单位长度
C.向左平移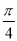 个单位长度 D.向右平移
个单位长度 D.向右平移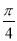 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省高三联合考试理科数学试卷(解析版) 题型:选择题
若两曲线在交点P处的切线互相垂直,则称该两曲线在点P处正交,设椭圆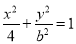
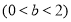 与双曲线
与双曲线 在交点处正交,则椭圆
在交点处正交,则椭圆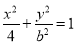 的离心率为( )
的离心率为( )
A.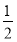 B.
B.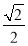 C.
C.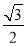 D.
D.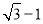
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省上饶市高三第二次模拟考试理科数学试卷(解析版) 题型:填空题
在数列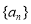 中,
中,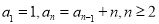 .为计算这个数列前10项的和S,现给出该问题算法的程序框图(如图所示),则图中判断框(1)处合适的语句是___________
.为计算这个数列前10项的和S,现给出该问题算法的程序框图(如图所示),则图中判断框(1)处合适的语句是___________
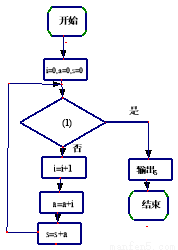
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com