Question

【题目】已知如图1，在Rt△ABC中，∠ACB=30°，∠ABC=90°，D为AC中点，AEBD于E，延长AE交BC于F，将△ABD沿BD折起，使平面ABD平面BCD，如图2所示。

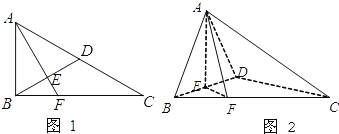
（Ⅰ）求证：AE平面BCD；

（Ⅱ）求二面角A-DC-B的余弦值；

（Ⅲ）求三棱锥B-AEF与四棱锥A-FEDC的体积的比（只需写出结果，不要求过程）．

Answer 1

【答案】（Ⅰ）证明见解析；（Ⅱ）；（Ⅲ）1:5

【解析】

（Ⅰ）由平面ABD⊥平面BCD，交线为BD，AE⊥BD于E，能证明AE⊥平面BCD;

（Ⅱ）以E为坐标原点，分别以EF、ED、EA所在直线为x轴，y轴，z轴，建立空间直角坐标系E-xyz，利用向量法求出二面角A-DC-B的余弦值;

（Ⅲ）利用体积公式分别求出三棱锥B-AEF与四棱锥A-FEDC的体积，再作比写出答案即可．

（Ⅰ）证明：∵平面ABD⊥平面BCD，交线为BD，

又在△ABD中，AE⊥BD于E，AE平面ABD，

∴AE⊥平面BCD．

（Ⅱ）由（1）知AE⊥平面BCD，∴AE⊥EF，

由题意知EF⊥BD，又AE⊥BD，

如图，以E为坐标原点，分别以EF、ED、EA所在直线为x轴，y轴，z轴，
建立空间直角坐标系E-xyz，

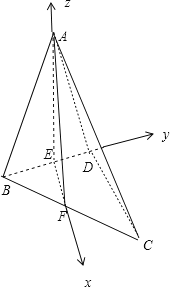
设AB=BD=DC=AD=2，
则BE=ED=1，∴AE=，BC=2，BF=，

则E（0，0，0），D（0，1，0），B（0，-1，0），A（0，0，），
F（，0，0），C（，2，0），

，，

由AE⊥平面BCD知平面BCD的一个法向量为，

设平面ADC的一个法向量，

则，取x=1，得，

∴，

∴二面角A-DC-B的平面角为锐角，故余弦值为．
（Ⅲ）三棱锥B-AEF与四棱锥A-FEDC的体积的比为：1:5.