练习册

  • 练习册
  • 试题
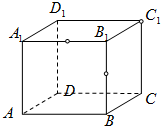    精英家教网 > 高中数学 > 题目详情

    正方体A-C1中，棱长为1，M在棱AB上，AM=1/3，P是面ABCD上的动点，P到线A1D1的距离与P到点M的距离平方差为1，则P点的轨迹以下哪条曲线上？  


    1. A.
      圆
    2. B.
      椭圆
    3. C.
      双曲线
    4. D.
      抛物线
    D

    解：如图所示：正方体ABCD-A1B1C1D1中，作PQ⊥AD，Q为垂足，则PQ⊥面ADD1A1，过点Q作QR⊥D1A1，
    则D1A1⊥面PQR，PR即为点P到直线A1D1的距离，由题意可得 PR2-PQ2=RQ2=4．
    又已知 PR2-PM2=4，
    ∴PM=PQ，即P到点M的距离等于P到AD的距离，根据抛物线的定义可得，点P的轨迹是抛物线，
    故选D．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    精英家教网在棱长为1的正方体ABCD-A1B1C1D1的密闭容器中，棱A1B1和棱BB1的中点处各有一个小孔，顶点C1处也有一个小孔，若正方体可任意放置，且小孔面积不计，则这个正方体容器中最多可容纳水的体积是（　　）
    A、
    3
    4
    B、
    7
    8
    C、
    23
    24
    D、
    26
    27

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，在棱长为1的正方体ABCD-A1B1C1D1中，E是棱BC的中点，点F是棱CD上的动点．
    （1）请用尺子把右边图形画在答题卡上
    （2）试确定点F的位置，使得D1E⊥平面AB1F
    （3）当D1E⊥平面AB1F时，求二面角C1-EF-A的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

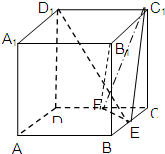    如图，在棱长为a的正方体ABCD-A1B1C1D1中，点E，F分别为棱BC，DC上的动点，且BE=CF．
    （1）求证：B1F⊥D1E；
    （2）当三棱锥C1-FCE的体积取到最大值时，求二面角C1-FE-C的正切值．

    查看答案和解析>>

    科目：高中数学 来源：2011年浙江省杭州市高二寒假作业数学理卷二 题型：选择题

    正方体A-C1中，棱长为1，M在棱AB上，AM=1/3，P是面ABCD上的动点，P到线A1D1的距离与P到点M的距离平方差为1，则P点的轨迹以下哪条曲线上？ （    ） 

         A．圆   B. 椭圆  C.双曲线   D.抛物线        

     

    查看答案和解析>>

    同步练习册答案