
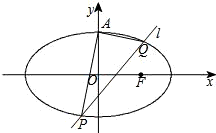
 如图,已知椭圆
如图,已知椭圆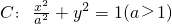 的上顶点为A,右焦点为F,直线AF与圆M:x2+y2-6x-2y+7=0相切.
的上顶点为A,右焦点为F,直线AF与圆M:x2+y2-6x-2y+7=0相切.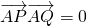 ,求证:直线l过定点,并求出该定点N的坐标.
,求证:直线l过定点,并求出该定点N的坐标.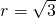 .(1分)
.(1分)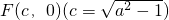
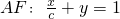 ,即x+cy-c=0,(2分)
,即x+cy-c=0,(2分)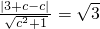 ,
,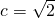 或
或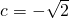 (舍去).(4分)
(舍去).(4分)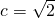 时,a2=c2+1=3,故椭圆C的方程为
时,a2=c2+1=3,故椭圆C的方程为 .(5分)
.(5分)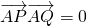 ,知AP⊥AQ,从而直线AP与坐标轴不垂直,(6分)
,知AP⊥AQ,从而直线AP与坐标轴不垂直,(6分) (7分)
(7分) 并整理得:(1+3k2)x2+6kx=0,
并整理得:(1+3k2)x2+6kx=0,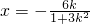 ,因此P的坐标为
,因此P的坐标为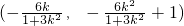 ,
,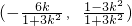 -(9分)
-(9分)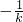 ,得Q
,得Q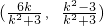 .-(10分)
.-(10分)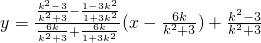 (11分)
(11分)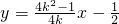 ,(13分)
,(13分)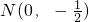 (14分)
(14分)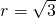 .由A(0,1),
.由A(0,1),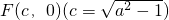 得直线
得直线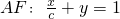 ,由直线AF与圆M相切,得
,由直线AF与圆M相切,得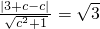 ,由此能求出椭圆C的方程.
,由此能求出椭圆C的方程.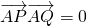 ,知AP⊥AQ,从而直线AP与坐标轴不垂直,由A(0,1)可设直线AP的方程为y=kx+1,直线AQ的方程为
,知AP⊥AQ,从而直线AP与坐标轴不垂直,由A(0,1)可设直线AP的方程为y=kx+1,直线AQ的方程为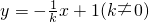 .将y=kx+1代入椭圆C的方程
.将y=kx+1代入椭圆C的方程 并整理得:(1+3k2)x2+6kx=0,解得x=0或
并整理得:(1+3k2)x2+6kx=0,解得x=0或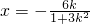 ,因此P的坐标为
,因此P的坐标为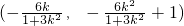 ,由此能证明直线l过定点,并能求出该定点N的坐标.
,由此能证明直线l过定点,并能求出该定点N的坐标.

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源:辽宁省铁岭高级中学2012届高三第一学期期中考试数学理科试题 题型:044
如图,已知椭圆![]() 的上顶点为A,右焦点为F,直线AF与圆
的上顶点为A,右焦点为F,直线AF与圆

(Ⅰ)求椭圆C的方程;
(Ⅱ)若不过点A的动直线l与椭圆C相交于P、Q两点,且![]() 求证:直线l过定点,并求出该定点N的坐标
求证:直线l过定点,并求出该定点N的坐标
查看答案和解析>>
科目:高中数学 来源:2010年高考试题分项版理科数学之专题六不等式 题型:解答题
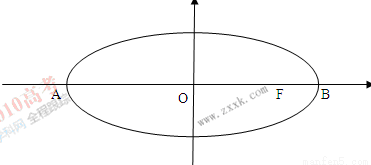
(16分)在平面直角坐标系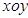 中,如图,已知椭圆
中,如图,已知椭圆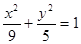 的左右顶点为A,B,右顶点为F,设过点T(
的左右顶点为A,B,右顶点为F,设过点T(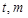 )的直线TA,TB与椭圆分别交于点M
)的直线TA,TB与椭圆分别交于点M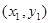 ,
,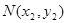 ,其中m>0,
,其中m>0,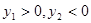
①设动点P满足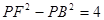 ,求点P的轨迹
,求点P的轨迹
②设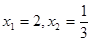 ,求点T的坐标
,求点T的坐标
③设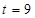 ,求证:直线MN必过x轴上的一定点
,求证:直线MN必过x轴上的一定点
(其坐标与m无关)
查看答案和解析>>
科目:高中数学 来源:2010年高考试题分项版理科数学之专题三数列 题型:解答题
(16分)在平面直角坐标系 中,如图,已知椭圆
中,如图,已知椭圆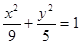 的左右顶点为A,B,右顶点为F,设过点T(
的左右顶点为A,B,右顶点为F,设过点T(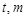 )的直线TA,TB与椭圆分别交于点M
)的直线TA,TB与椭圆分别交于点M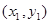 ,
,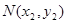 ,其中m>0,
,其中m>0,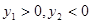

①设动点P满足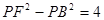 ,求点P的轨迹
,求点P的轨迹
②设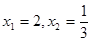 ,求点T的坐标
,求点T的坐标
③设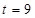 ,求证:直线MN必过x轴上的一定点
,求证:直线MN必过x轴上的一定点
(其坐标与m无关)
查看答案和解析>>
科目:高中数学 来源:2012年江苏省苏锡常镇四市高考数学一模试卷(解析版) 题型:解答题
 的上顶点为A,直线y=-4交椭圆E于点B,C(点B在点C的左侧),点P在椭圆E上.
的上顶点为A,直线y=-4交椭圆E于点B,C(点B在点C的左侧),点P在椭圆E上.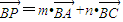 (m,n为实数),求m+n的最大值.
(m,n为实数),求m+n的最大值.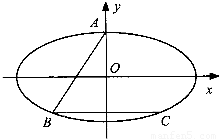
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com