考察下列式子：
，得出的一般性结论为________________________
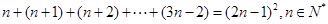
解析试题分析：由1=12=（2×1－1）2；
2+3+4=32=（2×2－1）2；
3+4+5+6+7=52=（2×3－1）2；
4+5+6+7+8+9+10=72=（2×4－1）2；
………
由上边的式子可以得出：第n个等式的左边的第一项为n，接下来依次加1，共有2n-1项，等式右边是2n－1的平方，
从而我们可以得出的一般性结论为：n+（n+1）+…+（2n－1）+…+（3n－2）=（2n－1）2（n∈N*）。
考点：本题主要考查归纳推理。
点评：归纳推理的一般步骤是：（1）通过观察个别情况发现某些相同性质；（2）从已知的相同性质中推出一个明确表达的一般性命题（猜想）．解题时要注意观察，善于总结．
科目：高中数学 来源： 题型：填空题
在平面几何里，有勾股定理：“设
的两边AB、AC互相垂直，则
。”拓展到空间，类比平面几何的勾股定理，研究三棱锥的侧面积与底面积间的关系，可以得到的正确结论是：“设三棱锥A-BCD的三个侧面ABC、ACD、ADB两两互相垂直，则 ”
查看答案和解析>>
科目：高中数学 来源： 题型：填空题
平面上有
条直线, 这条直线任意两条不平行, 任意三条不共点, 记这条直线将平面分成
部分, 则
___________, 
时,
_________________.)(用表示).
查看答案和解析>>
科目：高中数学 来源： 题型：填空题
如图所示,从中间阴影算起，图1表示蜂巢有1层只有一个室,图2表示蜂巢有2层共有7个室,图3表示蜂巢有3层共有19个室,图4表示蜂巢有4层共有37个室. 观察蜂巢的室的规律，指出蜂巢有n层时共有_______个室.
2107
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
：
, 则(1)
；
是第８个值等于1的项，则
.
，则依次类推可得
；
的三边长为
，内切圆半径为
（用
），则
；类比这一结论有：若三棱锥
的内切球半径为
，则三棱锥体积
， 
， 
， ……
个等式：
．
分别与实数
对应，则线段
的中点
与实数
对应，由此结论类比到平面得，若平面上不共线的三点
分别与二元实数对
对应，则
的重心
与 对应.