
 轴交于点O、A,与y轴交于点O、B,其中O为原点.(1)求证:△OAB的面积为定值;(2)设直线y = –2x+4与圆C交于点M, N,若OM = ON,求t的值并求出圆C的方程.
轴交于点O、A,与y轴交于点O、B,其中O为原点.(1)求证:△OAB的面积为定值;(2)设直线y = –2x+4与圆C交于点M, N,若OM = ON,求t的值并求出圆C的方程.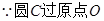 ,
,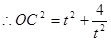 .
. 的方程是
的方程是 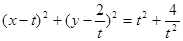
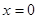 ,得
,得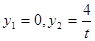 ;令
;令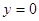 ,得
,得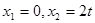
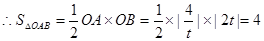 ,即:
,即: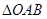 的面积为定值.------6分
的面积为定值.------6分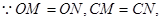
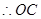 垂直平分线段
垂直平分线段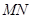 .
.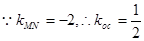 ,
,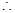 直线
直线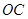 的方程是
的方程是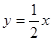 .
.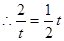 ,解得:
,解得: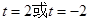 -----------------9分
-----------------9分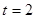 时,圆心
时,圆心 的坐标为
的坐标为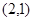 ,
,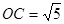 ,
,  到直线
到直线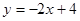 的距离
的距离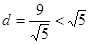 ,
, 与直线
与直线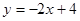 相交于两点。------------------12分. ----
相交于两点。------------------12分. ----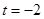 时,圆心
时,圆心 的坐标为
的坐标为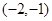 ,
,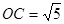 ,
, 到直线
到直线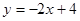 的距离
的距离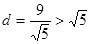
 与直线
与直线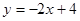 不相交,
不相交,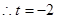 不符合题意舍去. ------------------14分
不符合题意舍去. ------------------14分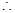 圆
圆 的方程为
的方程为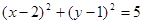 .------------15分
.------------15分 ,
,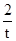 )2=t2+
)2=t2+ ,
,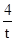 ,
,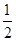 OA×OB=
OA×OB=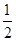 ×|
×|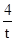 |×|2t|=4,
|×|2t|=4,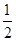 ,
,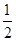 x,
x,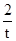 =
=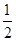 t,解得:t=2或t=-2,
t,解得:t=2或t=-2,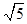
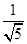 <
<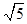 ,
,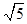 此时C到直线y=-2x+4的距离d=
此时C到直线y=-2x+4的距离d=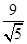 >
>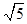 ,
,

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源:不详 题型:解答题
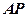 是⊙
是⊙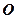 的切线,
的切线,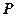 为切点,
为切点,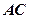 是⊙
是⊙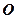 的割线,与⊙
的割线,与⊙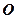 交于
交于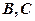 两点,圆心
两点,圆心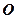 在
在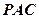 的内部,点
的内部,点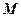 是
是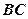 的中点。
的中点。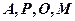 四点共圆;
四点共圆;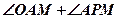 的大小。
的大小。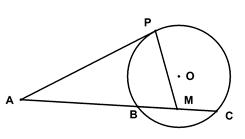
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com