
【题目】已知函数![]() 在区间
在区间![]() 内存在零点.
内存在零点.
(1)求![]() 的范围;
的范围;
(2)设![]() ,
,![]() 是
是![]() 的两个零点,求证:
的两个零点,求证:![]() .
.
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:高中数学 来源: 题型:
【题目】某组委会要从五名志愿者中选派四人分别从事翻译导游礼仪司机四项不同工作,若其中甲不能从事翻译工作,乙不能从事导游工作,其余三人均能从事这四项工作,则不同的选派方案共有________种.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,对一切
,对一切![]() ,点
,点![]() 都在函数
都在函数![]() 的图象上.
的图象上.
(1)求![]() ,归纳数列
,归纳数列![]() 的通项公式(不必证明).
的通项公式(不必证明).
(2)将数列![]() 依次按1项、2项、3项、4项循环地分为
依次按1项、2项、3项、4项循环地分为![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() ,…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为
,…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为![]() ,求
,求![]() 的值.
的值.
(3)设![]() 为数列
为数列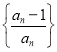 的前
的前![]() 项积,且
项积,且![]() ,求数列
,求数列![]() 的最大项.
的最大项.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E:![]() (a>b>0)的离心率e
(a>b>0)的离心率e![]() .
.
(1)若点P(1,![]() )在椭圆E上,求椭圆E的标准方程;
)在椭圆E上,求椭圆E的标准方程;
(2)若D(2,0)在椭圆内部,过点D斜率为![]() 的直线交椭圆E于M.N两点,|MD|=2|ND|,求椭圆E的方程.
的直线交椭圆E于M.N两点,|MD|=2|ND|,求椭圆E的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以数列![]() 的任意相邻两项为坐标的点
的任意相邻两项为坐标的点![]() ,均在一次函数y=2x+k的图象上,数列
,均在一次函数y=2x+k的图象上,数列![]() 满足
满足![]() ,且
,且![]() .
.
(1)求证数列![]() 为等比数列,并求出数列
为等比数列,并求出数列![]() 的公比;
的公比;
(2)设数列![]() ,
,![]() 的前n项和分别为Sn,Tn,若S6=T4,S5=﹣9,求k的值.
的前n项和分别为Sn,Tn,若S6=T4,S5=﹣9,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)射线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 两点(异于原点
两点(异于原点![]() ),定点
),定点![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先阅读参考材料,再解决此问题:
参考材料:求抛物线弧![]() (
(![]() )与x轴及直线
)与x轴及直线![]() 所围成的封闭图形的面积
所围成的封闭图形的面积
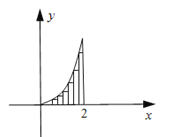
解:把区间![]() 进行n等分,得
进行n等分,得![]() 个分点
个分点![]() (
(![]() ),过分点
),过分点![]() ,作x轴的垂线,交抛物线于
,作x轴的垂线,交抛物线于![]() ,并如图构造
,并如图构造![]() 个矩形,先求出
个矩形,先求出![]() 个矩形的面积和
个矩形的面积和![]() ,再求
,再求![]() ,即是封闭图形的面积,又每个矩形的宽为
,即是封闭图形的面积,又每个矩形的宽为![]() ,第i个矩形的高为
,第i个矩形的高为![]() ,所以第i个矩形的面积为
,所以第i个矩形的面积为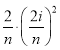 ;
;
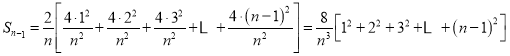
![]()
所以封闭图形的面积为![]()
阅读以上材料,并解决此问题:已知对任意大于4的正整数n,
不等式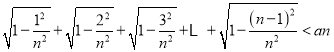 恒成立,
恒成立,
则实数a的取值范围为______
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在下列向量组中,可以把向量![]() =(3,2)表示出来的是( )
=(3,2)表示出来的是( )
A. ![]() =(0,0),
=(0,0),![]() =(1,2)B.
=(1,2)B. ![]() =(-1,2),
=(-1,2),![]() =(5,-2)
=(5,-2)
C. ![]() =(3,5),
=(3,5),![]() =(6,10)D.
=(6,10)D. ![]() =(2,-3),
=(2,-3),![]() =(-2,3)
=(-2,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的定义域为
的定义域为![]() ,如果存在非零常数
,如果存在非零常数![]() ,对于任意
,对于任意![]() ,都有
,都有![]() ,则称函数
,则称函数![]() 是“似周期函数”,非零常数
是“似周期函数”,非零常数![]() 为函数
为函数![]() 的“似周期”.现有下面四个关于“似周期函数”的命题:
的“似周期”.现有下面四个关于“似周期函数”的命题:
①如果“似周期函数”![]() 的“似周期”为-1,那么它是周期为2的周期函数;
的“似周期”为-1,那么它是周期为2的周期函数;
②函数![]() 是“似周期函数”;
是“似周期函数”;
③函数![]() 是“似周期函数”;
是“似周期函数”;
④如果函数![]() 是“似周期函数”,那么“
是“似周期函数”,那么“![]() ”.
”.
其中是真命题的序号是 .(写出所有满足条件的命题序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com