
【题目】已知函数![]() .
.
(1)确定函数![]() 在定义域上的单调性;
在定义域上的单调性;
(2)若![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减(2)
上单调递减(2)![]()
【解析】试题分析:(1)函数![]() 的定义域为
的定义域为![]() ,对其求导得
,对其求导得 ,令
,令![]() ,再利用导数判断
,再利用导数判断![]() 的单调性得其最大值为0,即
的单调性得其最大值为0,即![]() 在定义域上恒成立,故可得
在定义域上恒成立,故可得![]() 的单调性;(2)可将题意整理为
的单调性;(2)可将题意整理为![]() 在
在![]() 上恒成立,令
上恒成立,令![]() ,分为
,分为![]() ,
, ![]() 和
和![]() 三种情形分别进行讨论.
三种情形分别进行讨论.
试题解析:(1)函数![]() 的定义域为
的定义域为![]() ,
,  ,
,
令![]() ,则有
,则有![]() ,
,
令![]() ,解得
,解得![]() ,所以在
,所以在![]() 上,
上, ![]() ,
, ![]() 单调递增,
单调递增,
在![]() 上,
上, ![]() ,
, ![]() 单调递减.
单调递减.
又![]() ,所以
,所以![]() 在定义域上恒成立,即
在定义域上恒成立,即![]() 在定义域上恒成立,
在定义域上恒成立,
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(2)由![]() 在
在![]() 上恒成立得:
上恒成立得: ![]() 在
在![]() 上恒成立.
上恒成立.
整理得: ![]() 在
在![]() 上恒成立.
上恒成立.
令![]() ,易知,当
,易知,当![]() 时,
时, ![]() 在
在![]() 上恒成立不可能,∴
上恒成立不可能,∴![]() ,
,
又![]() ,
, ![]() ,
,
![]() 当
当![]() 时,
时, ![]() ,又
,又![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() 在
在![]() 上恒成立,则
上恒成立,则![]() 在
在![]() 上单调递减,又
上单调递减,又![]() ,所以
,所以![]() 在
在![]() 上恒成立.
上恒成立.
![]() 当
当![]() 时,
时, ![]() ,
, ![]() ,又
,又![]() 在
在![]() 上单调递减,所以存在
上单调递减,所以存在![]() ,使得
,使得![]() ,
,
所以在![]() 上
上![]() ,在
,在![]() 上
上![]() ,
,
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
又![]() ,所以
,所以![]() 在
在![]() 上恒成立,
上恒成立,
所以![]() 在
在![]() 上恒成立不可能.
上恒成立不可能.
综上所述, ![]() .
.


科目:高中数学 来源: 题型:
【题目】已知:①函数![]() ;
;
②向量![]() ,
,![]() ,且
,且![]() ,
,![]() ;
;
③函数![]() 的图象经过点
的图象经过点![]()
请在上述三个条件中任选一个,补充在下面问题中,并解答.
已知_________________,且函数![]() 的图象相邻两条对称轴之间的距离为
的图象相邻两条对称轴之间的距离为![]() .
.
(1)若![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(2)求函数![]() 在
在![]() 上的单调递减区间.
上的单调递减区间.
注:如果选择多个条件分别解答,按第一个解答计分.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区对12岁儿童瞬时记忆能力进行调查,瞬时记忆能力包括听觉记忆能力与视觉记忆能力。某班学生共有40人,下表为该班学生瞬时记忆能力的调查结果。例如表中听觉记忆能力为中等,且视觉记忆能力偏高的学生为3人。
视觉 听觉 | 视觉记忆能力 | ||||
偏低 | 中等 | 偏高 | 超常 | ||
听觉 记忆 能力 | 偏低 | 0 | 7 | 5 | 1 |
中等 | 1 | 8 | 3 | b | |
偏高 | 2 | a | 0 | 1 | |
超常 | 0 | 2 | 1 | 1 | |
由于部分数据丢失,只知道从这40位学生中随机抽取一个,视觉记忆能力恰为中等,且听觉记忆能力为中等或中等以上的概率为![]() 。
。
(1)试确定a,b的值;
(2)从40人中任意抽取3人,设具有听觉记忆能力或视觉记忆能力偏高或超常的学生人数为X,求随机变量X的分布列。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点
经过点![]() ,离心率为
,离心率为![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,
, ![]() .
.
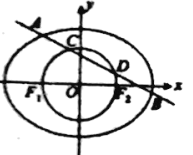
(1)求椭圆的方程;
(2)若直线![]() :
: ![]() 与椭圆交于
与椭圆交于![]() ,
, ![]() 两点,与以
两点,与以![]() 为直径的圆交于
为直径的圆交于![]() ,
, ![]() 两点,且满足
两点,且满足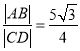 ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:①若直线![]() ,那么直线
,那么直线![]() 必平行于平面
必平行于平面![]() 内的无数条直线;②一个长为
内的无数条直线;②一个长为![]() ,宽为
,宽为![]() 的矩形,其直观图的面积为
的矩形,其直观图的面积为![]() ;③若函数
;③若函数![]() 的定义域是
的定义域是![]() ,则
,则![]() 的定义域是
的定义域是![]() ;④定义在
;④定义在![]() 上的函数
上的函数![]() ,若
,若![]() ,则函数
,则函数![]() 的图象关于点
的图象关于点![]() 中心对称.其中所有正确命题的编号为____________.
中心对称.其中所有正确命题的编号为____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是各项均为正数的等比数列,且a1+a2=6,a1a2=a3.
(1)求数列{an}的通项公式;
(2){bn}为各项非零的等差数列,其前n项和为Sn.已知S2n+1=bnbn+1,求数列{![]() }的前n项和Tn.
}的前n项和Tn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com