
【题目】若存在![]() ,使得
,使得![]() 对任意
对任意![]() 恒成立,则函数
恒成立,则函数![]() 在
在![]() 上有下界,其中
上有下界,其中![]() 为函数
为函数![]() 的一个下界;若存在
的一个下界;若存在![]() ,使得
,使得![]() 对任意
对任意![]() 恒成立,则函数
恒成立,则函数![]() 在
在![]() 上有上界,其中
上有上界,其中![]() 为函数
为函数![]() 的一个上界.如果一个函数既有上界又有下界,那么称该函数有界.下列四个结论:
的一个上界.如果一个函数既有上界又有下界,那么称该函数有界.下列四个结论:
①1不是函数![]() 的一个下界;②函数
的一个下界;②函数![]() 有下界,无上界;
有下界,无上界;
③函数![]() 有上界,无下界;④函数
有上界,无下界;④函数![]() 有界.
有界.
其中所有正确结论的编号为_______.
科目:高中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A.命题“若am2<bm2,则a<b”的逆命题是真命题
B.命题“存在x0∈R,x02﹣x0>0”的否定是“对任意的xR,x2﹣x≤0”
C.命题“p或q”为真命题,则命题p和命题q均为真命题
D.已知函数f(x)在R上可导,则f'(x0)=0是f(x0)为函数f(x)的极值”的必要不充分条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定椭圆![]() >
>![]() >0
>0![]() ,称圆心在原点
,称圆心在原点![]() ,半径为
,半径为![]() 的圆是椭圆
的圆是椭圆![]() 的“准圆”.若椭圆
的“准圆”.若椭圆![]() 的一个焦点为
的一个焦点为![]() ,其短轴上的一个端点到
,其短轴上的一个端点到![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的方程和其“准圆”方程;
的方程和其“准圆”方程;
(2)点![]() 是椭圆
是椭圆![]() 的“准圆”上的一个动点,过点
的“准圆”上的一个动点,过点![]() 作直线
作直线![]() ,使得
,使得![]() 与椭圆
与椭圆![]() 都只有一个交点.求证:
都只有一个交点.求证:![]() ⊥
⊥![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
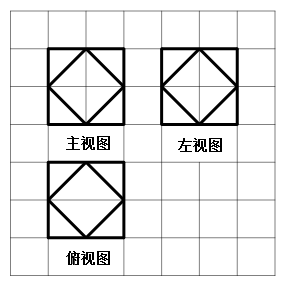
【题目】半正多面体(semiregular solid) 亦称“阿基米德多面体”,是由边数不全相同的正多边形为面的多面体,体现了数学的对称美.二十四等边体就是一种半正多面体,是由正方体切截而成的,它由八个正三角形和六个正方形为面的半正多面体.如图所示,图中网格是边长为1的正方形,粗线部分是某二十四等边体的三视图,则该几何体的体积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年12月以来,湖北武汉市发现多起病毒性肺炎病例,并迅速在全国范围内开始传播,专家组认为,本次病毒性肺炎病例的病原体初步判定为新型冠状病毒,该病毒存在人与人之间的传染,可以通过与患者的密切接触进行传染.我们把与患者有过密切接触的人群称为密切接触者,每位密切接触者被感染后即被称为患者.已知每位密切接触者在接触一个患者后被感染的概率为![]() ,某位患者在隔离之前,每天有
,某位患者在隔离之前,每天有![]() 位密切接触者,其中被感染的人数为
位密切接触者,其中被感染的人数为![]() ,假设每位密切接触者不再接触其他患者.
,假设每位密切接触者不再接触其他患者.
(1)求一天内被感染人数为![]() 的概率
的概率![]() 与
与![]() 、
、![]() 的关系式和
的关系式和![]() 的数学期望;
的数学期望;
(2)该病毒在进入人体后有14天的潜伏期,在这14天的潜伏期内患者无任何症状,为病毒传播的最佳时间,设每位患者在被感染后的第二天又有![]() 位密切接触者,从某一名患者被感染,按第1天算起,第
位密切接触者,从某一名患者被感染,按第1天算起,第![]() 天新增患者的数学期望记为
天新增患者的数学期望记为![]() .
.
(i)求数列![]() 的通项公式,并证明数列
的通项公式,并证明数列![]() 为等比数列;
为等比数列;
(ii)若戴口罩能降低每位密切接触者患病概率,降低后的患病概率![]() ,当
,当![]() 取最大值时,计算此时
取最大值时,计算此时![]() 所对应的
所对应的![]() 值和此时
值和此时![]() 对应的
对应的![]() 值,根据计算结果说明戴口罩的必要性.(取
值,根据计算结果说明戴口罩的必要性.(取![]() )
)
(结果保留整数,参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人在政治、历史、地理、物理、化学、生物、技术7门学科中任选3门.若同学甲必选物理,则下列说法正确的是( )
A.甲、乙、丙三人至少一人选化学与全选化学是对立事件
B.甲的不同的选法种数为15
C.已知乙同学选了物理,乙同学选技术的概率是![]()
D.乙、丙两名同学都选物理的概率是![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com