
 平面ACB1)作垂直于D1B的平面分别交过D1的三条棱于E、F、G.
平面ACB1)作垂直于D1B的平面分别交过D1的三条棱于E、F、G.
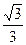 ·a
·a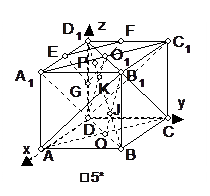
 =(-a,-a,a),
=(-a,-a,a),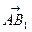 =(0,a,a),
=(0,a,a),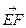 (-xE,yF,0),
(-xE,yF,0),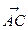 =(-a,a,0),
=(-a,a,0),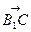 =(-a,0,-a),
=(-a,0,-a), ·
·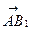 =(-a,-a,a)·(0,a,a)=0,
=(-a,-a,a)·(0,a,a)=0, ⊥
⊥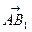 ,
, ⊥
⊥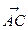 ,
,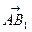 与
与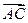 不共线且相交于点A,
不共线且相交于点A, ⊥平面ACB1,又已知
⊥平面ACB1,又已知 ⊥平面EFG,
⊥平面EFG, ⊥平面EFG,所以
⊥平面EFG,所以 ⊥
⊥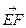 ,
, ·
·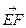 =0,
=0, 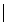
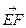
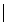 =
=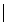
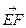
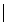 =
=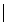
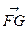
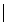 ,
,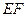 =A1C1=
=A1C1=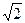 ·a,
·a,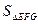 =
=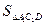
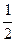
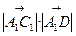 ·sin600
·sin600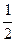 (
(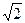 ·a)2·
·a)2·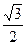
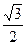 ·a2 .
·a2 .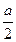 ,
,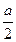 ,a),H(a,a,
,a),H(a,a,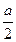 ),而
),而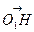 作为平面A1C1D的法向量,
作为平面A1C1D的法向量,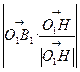 =
=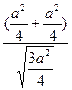 =
=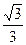 ·a.
·a.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源:不详 题型:解答题
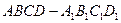 的棱长为
的棱长为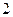 ,
,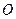 是
是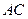 与
与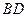 的交点,
的交点,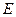 是
是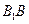 上一点,且
上一点,且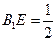 .(Ⅰ)求证:
.(Ⅰ)求证: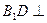 平面
平面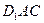 ;
;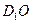 与
与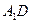 所成角的余弦值;
所成角的余弦值;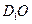 与平面
与平面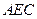 所成角的正弦值.
所成角的正弦值.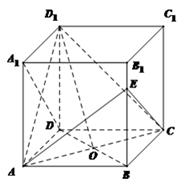
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
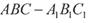 的侧棱与底面垂直,
的侧棱与底面垂直,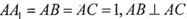 ,MN分别是
,MN分别是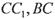 的中点,P点在
的中点,P点在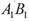 上,且满足
上,且满足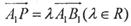
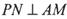
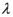 取何值时,直线PN与平面ABC所成的角
取何值时,直线PN与平面ABC所成的角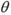 最大?并求出该最大角的正切值;
最大?并求出该最大角的正切值;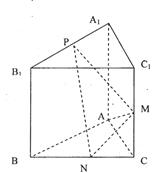
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
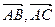 为一组邻边的平行四边形的面积S;
为一组邻边的平行四边形的面积S; 分别与向量
分别与向量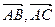 垂直,且
垂直,且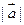 =
=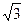 ,求向量
,求向量 的坐标。
的坐标。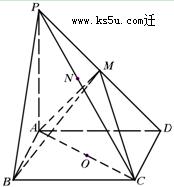
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com