
【题目】如图,三棱柱![]() 中,
中, ![]() 平面
平面![]() 分别为
分别为![]() 和
和![]() 的中点,
的中点, ![]() 是边长为
是边长为![]() 的正三角形,
的正三角形, ![]() .
.
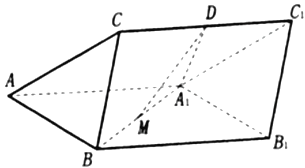
(1)证明: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
科目:高中数学 来源: 题型:
【题目】运货卡车以每小时x千米的速度匀速行驶130千米,按交通法规限制50≤x≤100(单位:千米/时).假设汽油的价格是每升2元,而汽车每小时耗油 升,司机的工资是每小时14元.
升,司机的工资是每小时14元.
(1)求这次行车总费用y关于x的表达式;
(2)当x为何值时,这次行车的总费用最低,并求出最低费用的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图如下图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6到5.0之间的学生数为b,则a,b的值分别为 ( )
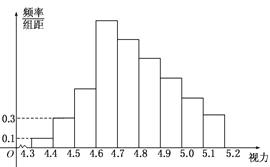
A. 0.27,78 B. 0.27,83 C. 2.7,78 D. 2.7,83
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查中小学课外使用互联网的情况,教育部向华东、华北、华南和西部地区60所中小学发出问卷![]() 份,
份, ![]() 名学生参加了问卷调查,并根据所得数据画出样本的频率分布直方图(如图).
名学生参加了问卷调查,并根据所得数据画出样本的频率分布直方图(如图).
(1)要从这![]() 名中小学中用分层抽样的方法抽取
名中小学中用分层抽样的方法抽取![]() 名中小学生进一步调查,则在
名中小学生进一步调查,则在![]() (小时)时间段内应抽出的人数是多少?
(小时)时间段内应抽出的人数是多少?
(2)若希望![]() 的中小学生每天使用互联网时间不少于
的中小学生每天使用互联网时间不少于![]() (小时),请估计
(小时),请估计![]() 的值,并说明理由.
的值,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com