
【题目】已知A是圆锥的顶点,BD是圆锥底面的直径,C是底面圆周上一点,AC=BD=2,BC=1,点M在线段BD上,且BM![]() ,平面ABC和平面ACD将圆锥截去部分后的几何体如图所示.
,平面ABC和平面ACD将圆锥截去部分后的几何体如图所示.
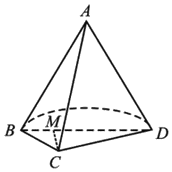
(1)求证:CM⊥AD;
(2)求AC与底面所成的角;
(3)求该几何体的体积.
【答案】(1)证明见解析(2)60°(3)![]()
【解析】
(1)在![]() 中通过解三角形得
中通过解三角形得![]() ,从而可证
,从而可证![]() 与平面
与平面![]() 垂直(取
垂直(取![]() 中点
中点![]() ,
,![]() 是圆锥的高),得线线垂直;
是圆锥的高),得线线垂直;
(2)由(1)![]() 是直线
是直线![]() 与底面所成的角,在三角形中求解即可;
与底面所成的角,在三角形中求解即可;
(3)该几何体是半个圆锥和一个三棱锥的组合体,由锥体体积公式计算.
(1)证明:∵C是底面圆周上一点,
∴BC⊥BD,
又∵![]() ,
,
∴∠BDC=30°,
∴∠CBD=60°,
在三角形BCM中,由余弦定理得:![]() ,
,
∴BC2=BM2+CM2,
∴CM⊥BD,
设O为BD的中点,连接AO,则AO⊥平面BCD,
∵CM在平面BCD内,
∴CM⊥AO,
又AO∩BD=O,
∴CM⊥平面BAD,
又AD在平面BAD内,
∴CM⊥AD;
(2)设O为BD的中点,连接CO,AO,则∠ACO为AC与底面所成的角,
由已知可得AB=AD=AC=BD=2,所以△ABD为正三角形,![]() ,
,
而CO=1,所以![]() ,
,
∴AC与底面所成的角为60°;
(3)由题设知,∠CBD=60°,
故△BCD的面积![]() ,
,
底面半圆的面积![]() ,
,
所以该几何体的体积![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如果对于函数f(x)定义域内任意的两个自变量的值x1,x2,当x1<x2时,都有f(x1)≤f(x2),且存在两个不相等的自变量值y1,y2,使得f(y1)=f(y2),就称f(x)为定义域上的不严格的增函数.则①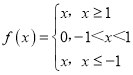 ,②
,②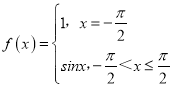 ,③
,③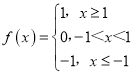 ,④
,④![]() ,四个函数中为不严格增函数的是_____,若已知函数g(x)的定义域、值域分别为A、B,A={1,2,3},BA,且g(x)为定义域A上的不严格的增函数,那么这样的g(x)有_____个.
,四个函数中为不严格增函数的是_____,若已知函数g(x)的定义域、值域分别为A、B,A={1,2,3},BA,且g(x)为定义域A上的不严格的增函数,那么这样的g(x)有_____个.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系。已知曲线C的极坐标方程为![]() ,过点
,过点![]() 的直线l的参数方程为
的直线l的参数方程为 (为参数),直线l与曲线C交于M、N两点。
(为参数),直线l与曲线C交于M、N两点。
(1)写出直线l的普通方程和曲线C的直角坐标方程:
(2)若![]() 成等比数列,求a的值。
成等比数列,求a的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校举行运动会,其中三级跳远的成绩在![]() 米以上的进入决赛,把所得的成绩进行整理后,分成
米以上的进入决赛,把所得的成绩进行整理后,分成![]() 组画出频率分布直方图的一部分(如图),已知第
组画出频率分布直方图的一部分(如图),已知第![]() 组的频数是
组的频数是![]() .
.
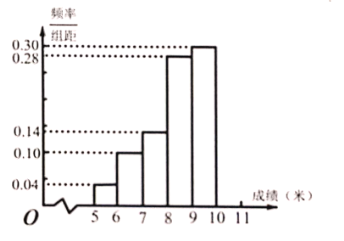
(1)求进入决赛的人数;
(2)用样本的频率代替概率,记![]() 表示两人中进入决赛的人数,求
表示两人中进入决赛的人数,求![]() 得分布列及数学期望.
得分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校举行运动会,其中三级跳远的成绩在![]() 米以上的进入决赛,把所得的数据进行整理后,分成
米以上的进入决赛,把所得的数据进行整理后,分成![]() 组画出频率分布直方图的一部分(如图),已知第
组画出频率分布直方图的一部分(如图),已知第![]() 组的频数是
组的频数是![]() .
.
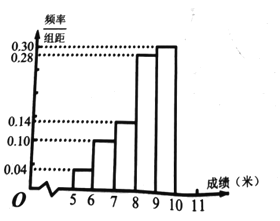
(1)求进入决赛的人数;
(2)经过多次测试后发现,甲的成绩均匀分布在![]() 米之间,乙的成绩均匀分布在
米之间,乙的成绩均匀分布在![]() 米之间,现甲、乙各跳一次,求甲比乙远的概率.
米之间,现甲、乙各跳一次,求甲比乙远的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《周髀算经》中给出了勾股定理的绝妙证明.如图是赵爽弦图及注文.弦图是一个以勾股形之弦为边的正方形,其面积称为弦实.图中包含四个全等的勾股形及一个小正方形,分别涂成朱色及黄色,其面积称为朱实、黄实.由2×勾×股+(股-勾)2=4×朱实+黄实=弦实,化简得勾2+股2=弦2.若图中勾股形的勾股比为![]() ,向弦图内随机抛掷100颗图钉(大小忽略不计),则落在黄色图形内的图钉颗数大约为( )(参考数据:
,向弦图内随机抛掷100颗图钉(大小忽略不计),则落在黄色图形内的图钉颗数大约为( )(参考数据:![]() ,
,![]() )
)
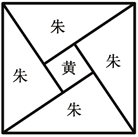
A.2B.4C.6D.8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某地某月1日至15日的日平均温度变化的折线图,根据该折线图,下列结论正确的是( )
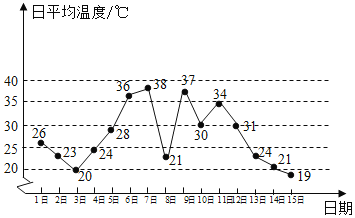
A. 这15天日平均温度的极差为![]()
B. 连续三天日平均温度的方差最大的是7日,8日,9日三天
C. 由折线图能预测16日温度要低于![]()
D. 由折线图能预测本月温度小于![]() 的天数少于温度大于
的天数少于温度大于![]() 的天数
的天数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】依照某发展中国家2018年的官方资料,将该国所有家庭按年收入从低到高的顺序平均分为五组,依次为第一组至第五组,各组家庭的年收入总和占该国全部家庭的年收入总和的百分比如图所示.
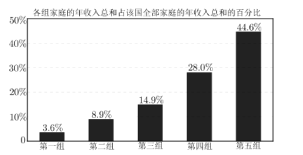
以下关于该国2018年家庭收入的判断,一定正确的是( )
A. 至少有![]() 的家庭的年收入都低于全部家庭的平均年收入
的家庭的年收入都低于全部家庭的平均年收入
B. 收入最低的那![]() 的家庭平均年收入为全部家庭平均年收入的
的家庭平均年收入为全部家庭平均年收入的![]()
C. 收入最高的那![]() 的家庭年收入总和超过全部家庭年收入总和的
的家庭年收入总和超过全部家庭年收入总和的![]()
D. 收入最低的那![]() 的家庭年收入总和超过全部家庭年收入总和的
的家庭年收入总和超过全部家庭年收入总和的![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别为△ABC三个内角A,B,C的对边,且acos C+![]() asin C-b-c=0.
asin C-b-c=0.
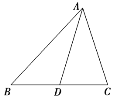
(1)求A;
(2)若AD为BC边上的中线,cos B=![]() ,AD=
,AD=![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com