
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
(本题满分12分)某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元.
(1)分别写出两种产品的收益与投资的函数关系;
(2)该家庭现有20万元资金,全部用于理财投资,问:怎样分配资金能使投资获得最大收益,其最大收益为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某化工企业2010年底投入100万元,购入一套污水处理设备.该设备每年的运转费用是0.5万元,此外每年都要花费一定的维护费,第一年的维护费为2万元,由于设备老化,以后每年的维护费都比上一年增加2万元.
(Ⅰ)求该企业使用该设备x年的年平均污水处理费用y(万元);
(Ⅱ)问为使该企业的年平均污水处理费用最低,该企业几年后需要重新更换新的污水处理设备?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某企业生产甲、乙两种产品, 根据市场调查与预测, 甲产品的利润与投资成正比, 其关系如图1, 乙产品的利润与投资的算术平方根成正比, 其关系如图2 (注: 利润与投资的单位: 万元).
(Ⅰ) 分别将甲、乙两种产品的利润表示为投资的函数关系式;
(Ⅱ) 该企业筹集了100万元资金投入生产甲、乙两种产品, 问: 怎样分配这100万元资金, 才能使企业获得最大利润, 其最大利润为多少万元?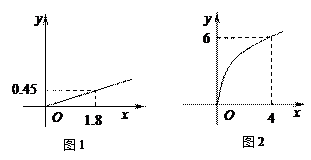
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图等腰梯形ABCD的两底分别为AB=10,CD=4,两腰AD=CB=5,动点P由B点沿折线BCDA向A运动,设P点所经过的路程为x,三角形ABP的面积为S.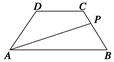
(1)求函数S=f(x)的解析式;
(2)试确定点P的位置,使△ABP的面积S最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com