
【题目】点O是平面上一定点,A、B、C是平面上△ABC的三个顶点,∠B、∠C分别是边AC、AB的对角,以下命题正确的是(把你认为正确的序号全部写上). ①动点P满足 ![]() =
= ![]() +
+ ![]() +
+ ![]() ,则△ABC的重心一定在满足条件的P点集合中;
,则△ABC的重心一定在满足条件的P点集合中;
②动点P满足 ![]() =
= ![]() +λ(
+λ( ![]() +
+ ![]() )(λ>0),则△ABC的内心一定在满足条件的P点集合中;
)(λ>0),则△ABC的内心一定在满足条件的P点集合中;
③动点P满足 ![]() =
= ![]() +λ(
+λ( 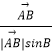 +
+ 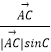 )(λ>0),则△ABC的重心一定在满足条件的P点集合中;
)(λ>0),则△ABC的重心一定在满足条件的P点集合中;
④动点P满足 ![]() =
= ![]() +λ(
+λ( 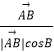 +
+ 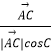 )(λ>0),则△ABC的垂心一定在满足条件的P点集合中;
)(λ>0),则△ABC的垂心一定在满足条件的P点集合中;
⑤动点P满足 ![]() =
= ![]() +λ(
+λ( 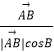 +
+ 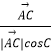 )(λ>0),则△ABC的外心一定在满足条件的P点集合中.
)(λ>0),则△ABC的外心一定在满足条件的P点集合中.
【答案】①②③④⑤
【解析】解:对于①,∵动点P满足 ![]() =
= ![]() +
+ ![]() +
+ ![]() , ∴
, ∴ ![]() =
= ![]() +
+ ![]() ,
,
则点P是△ABC的重心,故①正确;
对于②,∵动点P满足 ![]() =
= ![]() +λ(
+λ( ![]() +
+ ![]() )(λ>0),
)(λ>0),
∴ ![]() =λ(
=λ( ![]() +
+ ![]() )(λ>0),
)(λ>0),
又 ![]() +
+ ![]() 在∠BAC的平分线上,
在∠BAC的平分线上,
∴ ![]() 与∠BAC的平分线所在向量共线,
与∠BAC的平分线所在向量共线,
∴△ABC的内心在满足条件的P点集合中,②正确;
对于③,动点P满足 ![]() =
= ![]() +λ(
+λ( 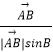 +
+ 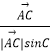 )(λ>0),
)(λ>0),
∴ ![]() =λ(
=λ( 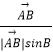 +
+ 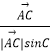 ),(λ>0),
),(λ>0),
过点A作AD⊥BC,垂足为D,则| ![]() |sinB=|
|sinB=| ![]() |sinC=AD,
|sinC=AD,![]() =
= ![]() (
( ![]() +
+ ![]() ),向量
),向量 ![]() +
+ ![]() 与BC边的中线共线,
与BC边的中线共线,
因此△ABC的重心一定在满足条件的P点集合中,③正确;
对于④,动点P满足 ![]() =
= ![]() +λ(
+λ( 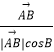 +
+ 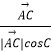 )(λ>0),
)(λ>0),
∴ ![]() =λ(
=λ( 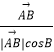 +
+ 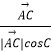 )(λ>0),
)(λ>0),
∴ ![]()
![]() =λ(
=λ( 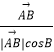 +
+ 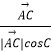 )
) ![]() =λ(|
=λ(| ![]() |﹣|
|﹣| ![]() |)=0,
|)=0,
∴ ![]() ⊥
⊥ ![]() ,
,
∴△ABC的垂心一定在满足条件的P点集合中,④正确;
对于⑤,动点P满足 ![]() =
= ![]() +λ(
+λ( 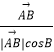 +
+ 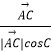 )(λ>0),
)(λ>0),
设 ![]() =
= ![]() ,
,
则 ![]() =λ(
=λ( 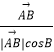 +
+ 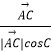 ),
),
由④知( 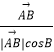 +
+ 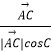 )
) ![]() =0,
=0,
∴ ![]()
![]() =0,
=0,
∴ ![]() ⊥
⊥ ![]() ,
,
∴P点的轨迹为过E的BC的垂线,即BC的中垂线;
∴△ABC的外心一定在满足条件的P点集合,⑤正确.
故正确的命题是①②③④⑤.
所以答案是:①②③④⑤.
【考点精析】根据题目的已知条件,利用命题的真假判断与应用的相关知识可以得到问题的答案,需要掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.


 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:高中数学 来源: 题型:
【题目】已知a>0,设命题p:函数y=ax在R上单调递增;命题q:不等式ax2﹣ax+1>0对x∈R恒成立,若p且q为假,p或q为真,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=sin(2x+ ![]() )+
)+ ![]() cos(2x+
cos(2x+ ![]() ),则( )
),则( )
A.y=f(x)在(0, ![]() )单调递增,其图象关于直线x=
)单调递增,其图象关于直线x= ![]() 对称
对称
B.y=f(x)在(0, ![]() )单调递增,其图象关于直线x=
)单调递增,其图象关于直线x= ![]() 对称
对称
C.y=f(x)在(0, ![]() )单调递减,其图象关于直线x=
)单调递减,其图象关于直线x= ![]() 对称
对称
D.y=f(x)在(0, ![]() )单调递减,其图象关于直线x=
)单调递减,其图象关于直线x= ![]() 对称
对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC是一个面积较大的三角形,点P是△ABC所在平面内一点且 ![]() +
+ ![]() +2
+2 ![]() =
= ![]() ,现将3000粒黄豆随机抛在△ABC内,则落在△PBC内的黄豆数大约是 .
,现将3000粒黄豆随机抛在△ABC内,则落在△PBC内的黄豆数大约是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥P﹣ABCD中,PD⊥平面ABCD,BC⊥CD,PD=1,AB= ![]() ,BC=CD=
,BC=CD= ![]() ,AD=1.
,AD=1. 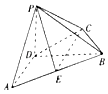
(1)求异面直线AB、PC所成角的余弦值;
(2)点E是线段AB的中点,求二面角E﹣PC﹣D的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,D、E分别是△ABC的三等分点,设 ![]() =
= ![]() ,
, ![]() =
= ![]() ,∠BAC=
,∠BAC= ![]() .
.
(1)用 ![]() ,
, ![]() 分别表示
分别表示 ![]() ,
, ![]() ;
;
(2)若 ![]()
![]() =15,|
=15,| ![]() |=3
|=3 ![]() ,求△ABC的面积.
,求△ABC的面积. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,为测一树的高度,在地面上选取A、B两点,从A、B两点分别测得树尖的仰角为30°、45°,且A、B两点之间的距离为60m,则树的高度为( ) 
A.(30+30 ![]() ) m
) m
B.(30+15 ![]() ) m??
) m??
C.(15+30 ![]() ) m
) m
D.(15+15 ![]() ) m
) m
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中真命题为( )
A.过点P(x0 , y0)的直线都可表示为y﹣y0=k(x﹣x0)
B.过两点(x1 , y1),(x2 , y2)的直线都可表示为(x﹣x1)(y2﹣y1)=(y﹣y1)(x2﹣x1)
C.过点(0,b)的所有直线都可表示为y=kx+b
D.不过原点的所有直线都可表示为 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com