
【题目】某校高三共有1000位学生,为了分析某次的数学考试成绩,采取随机抽样的方法抽取了50位高三学生的成绩进行统计分析,得到如图所示频数分布表:
分组 |
|
|
|
|
|
频数 | 3 | 11 | 18 | 12 | 6 |
(1)根据频数分布表计算成绩在![]() 的频率并计算这组数据的平均值
的频率并计算这组数据的平均值![]() (同组的数据用该组区间的中点值代替);
(同组的数据用该组区间的中点值代替);
(2)用分层抽样的方法从成绩在![]() 和
和![]() 的学生中共抽取5人,从这5人中任取2人,求成绩在
的学生中共抽取5人,从这5人中任取2人,求成绩在![]() 和
和![]() 中各有1人的概率.
中各有1人的概率.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
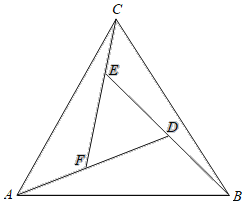
【题目】赵爽是我国汉代数学家、天文学家,他在注解《周髀算经》时,介绍了“勾股圆方图”,亦称“赵爽弦图”,它被2002年国际数学家大会选定为会徽.“赵爽弦图”是以弦为边长得到的正方形,该正方形由4个全等的直角三角形加上中间一个小正方形组成类比“赵爽弦图”,可类似地构造如图所示的图形它是由3个全等的三角形与中间的一个小等边三角形拼成的一个大等边三角形设DF=2AF=2,若在大等边三角形中随机取一点,则此点取自三个全等三角形(阴影部分)的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,函数
,函数![]() 在
在![]() ,
,![]() 处取得极值,其中
处取得极值,其中![]() .
.
(1)求实数t的取值范围;
(2)判断![]() 在
在![]() 上的单调性并证明;
上的单调性并证明;
(3)已知![]() 在
在![]() 上的任意
上的任意![]() 、
、![]() ,都有
,都有![]() ,令
,令![]() ,若函数
,若函数![]() 有3个不同的零点,求实数m的取值范围.
有3个不同的零点,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面ABCD是平行四边形,∠BCD=135°,PA⊥平面ABCD,AB=AC=PA=2,E,F,M分别为线段BC,AD,PD的中点.
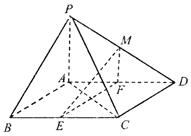
(1)求证:直线EF⊥平面PAC;
(2)求平面MEF与平面PBC所成二面角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线l的参数方程为
中,直线l的参数方程为![]() (t为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]()
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)若直线l与曲线C相交于A,B两点.求![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com