
分析 (1)解(a2+2)x2-2ax得:x=0,或x=$\frac{2a}{{a}^{2}+2}$,分别讨论$\frac{2a}{{a}^{2}+2}$与0的关系,结合二次函数的性质,可得不等式f(x)≤0的解集;
(2)由韦达定理的推论2得:|x1-x2|=$\frac{\left|2a\right|}{{a}^{2}+2}$,构造函数g(x)=$\frac{\left|2x\right|}{{x}^{2}+2}$=$\left\{\begin{array}{l}\frac{-2x}{{x}^{2}+2},x<0\\ \frac{2x}{{x}^{2}+2},x≥0\end{array}\right.$,利用导数法求其最大值,可得答案.
解答 解:(1)∵a2+2>0,
解(a2+2)x2-2ax得:x=0,或x=$\frac{2a}{{a}^{2}+2}$,
当a<0时,$\frac{2a}{{a}^{2}+2}$<0,不等式f(x)≤0的解集为:[$\frac{2a}{{a}^{2}+2}$,0],
当a=0时,$\frac{2a}{{a}^{2}+2}$=0,不等式f(x)≤0的解集为:{0},
当a>0时,$\frac{2a}{{a}^{2}+2}$>0,不等式f(x)≤0的解集为:[0,$\frac{2a}{{a}^{2}+2}$];
(2)若函数f(x)有两个零点x1,x2,
由韦达定理的推论2得:|x1-x2|=$\frac{\left|2a\right|}{{a}^{2}+2}$,
令g(x)=$\frac{\left|2x\right|}{{x}^{2}+2}$=$\left\{\begin{array}{l}\frac{-2x}{{x}^{2}+2},x<0\\ \frac{2x}{{x}^{2}+2},x≥0\end{array}\right.$,
则g′(x)=$\left\{\begin{array}{l}\frac{2{x}^{2}-4}{{(x}^{2}+2)^{2}},x<0\\ \frac{-2{x}^{2}+4}{{(x}^{2}+2)^{2}},x≥0\end{array}\right.$,
令g′(x)=0,则x=$±\sqrt{2}$,
当x$<-\sqrt{2}$,或0$<x<\sqrt{2}$时,g′(x)>0,函数为增函数;
当$-\sqrt{2}<x<0$,或x$>\sqrt{2}$时,g′(x)<0,函数为减函数;
故当x=$±\sqrt{2}$时,g(x)取最大值$\frac{\sqrt{2}}{2}$,
即|x1-x2|的最大值为$\frac{\sqrt{2}}{2}$.
点评 本题考查的知识点是二次函数的图象和性质,分类讨论思想,分段函数的应用,函数的最值,难度中档.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
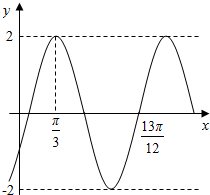 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$,x∈R)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$,x∈R)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | -2 | C. | 2 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com