
【题目】某大学生在开学季准备销售一种文具套盒进行试创业,在一个开学季内,每售出1盒该产品获利润50元;未售出的产品,每盒亏损30元![]() 根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示,该同学为这个开学季购进了160盒该产品,以
根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示,该同学为这个开学季购进了160盒该产品,以![]() 单位:盒,
单位:盒,![]() 表示这个开学季内的市场需求量,
表示这个开学季内的市场需求量,![]() 单位:元
单位:元![]() 表示这个开学季内经销该产品的利润
表示这个开学季内经销该产品的利润
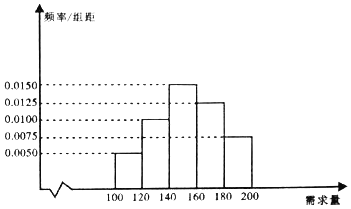
![]() 根据直方图估计这个开学季内市场需求量x的平均数和众数;
根据直方图估计这个开学季内市场需求量x的平均数和众数;
![]() 将y表示为x的函数;
将y表示为x的函数;
![]() 根据直方图估计利润不少于4800元的概率.
根据直方图估计利润不少于4800元的概率.
【答案】(1)153,150(2)y=![]() ,(3)0.9
,(3)0.9
【解析】
试题(1)以各组的中间值为各组需求量的代表值,计算出各组的频率为概率,频率最大对应的需求量即为需求量的众数,各组代表需求量与对应的频率的和就是需求量的平均数;(2)由已知条件推导出当100≤x≤160时,y=50x-(160-x)30=80x-1800,当160<x≤200时,y=160×50=8000,由此能将Y表示为X的函数,(3)根据(2)中利润与需求量的关系式,令y大于等于4800,列出关于需求量的不等式,求出需求量x的取值范围,再根据题中的频率分布表计算出对应的概率.
试题解析:(1)由频率直方图得到:
需求量为110的频率=0.005×20=0.1,
需求量为130的频率=0.01×20=0.2,
需求量为150的频率=0.015×20=0.3,
需求量为170的频率=0.0125×20=0.25,
需求量为190的频率=0.0075×20=0.15,
∴这个开学季内市场需求量X的众数是150,
这个开学季内市场需求量X的平均数:
![]() =110×0.1+130×0.2+150×0.3+170×0.25+190×0.15=153. 4分
=110×0.1+130×0.2+150×0.3+170×0.25+190×0.15=153. 4分
(2)∵每售出1盒该产品获利润50元,未售出的产品,每盒亏损30元,
∴当100≤x≤160时,
y=50x-(160-x)30=80x-1800,
当160<x≤200时,
y=160×50=8000,
∴y=![]() 8分
8分
(3)∵利润不少于4800元,
∴80x-4800≥4800,解得x≥120,
∴由(1)知利润不少于4800元的概率p=1-0.1=0.9. 12分
考点:离散型随机变量的期望与方差,频率分布直方图应用,众数、中位数、平均数,分段函数函数解析式,概率的估计


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴为正半轴为极轴建立极坐标系.已知曲线
轴为正半轴为极轴建立极坐标系.已知曲线![]() 的极坐标方程为
的极坐标方程为![]()
![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,直线
两点,直线![]() 过定点
过定点![]() 且倾斜角为
且倾斜角为![]() 交曲线
交曲线![]() 于
于![]() 两点.
两点.
(1)把曲线![]() 化成直角坐标方程,并求
化成直角坐标方程,并求![]() 的值;
的值;
(2)若![]() 成等比数列,求直线
成等比数列,求直线![]() 的倾斜角
的倾斜角![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C1:![]() y2=1的左右顶点是双曲线C2:
y2=1的左右顶点是双曲线C2:![]() 的顶点,且椭圆C1的上顶点到双曲线C2的渐近线的距离为
的顶点,且椭圆C1的上顶点到双曲线C2的渐近线的距离为![]() .
.
(1)求双曲线C2的方程;
(2)若直线与C1相交于M1,M2两点,与C2相交于Q1,Q2两点,且![]()
![]() 5,求|M1M2|的取值范围.
5,求|M1M2|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 九章算术
九章算术![]() 给出求羡除体积的“术”是:“并三广,以深乘之,又以袤乘之,六而一”,其中的“广”指羡除的三条平行侧棱的长,“深”指一条侧棱到另两条侧棱所在平面的距离,“袤”指这两条侧棱所在平行线之间的距离,用现代语言描述:在羡除
给出求羡除体积的“术”是:“并三广,以深乘之,又以袤乘之,六而一”,其中的“广”指羡除的三条平行侧棱的长,“深”指一条侧棱到另两条侧棱所在平面的距离,“袤”指这两条侧棱所在平行线之间的距离,用现代语言描述:在羡除![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,两条平行线
,两条平行线![]() 与
与![]() 间的距离为h,直线
间的距离为h,直线![]() 到平面
到平面![]() 的距离为
的距离为![]() ,则该羡除的体积为
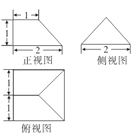
,则该羡除的体积为![]() 已知某羡除的三视图如图所示,则该羡除的体积为
已知某羡除的三视图如图所示,则该羡除的体积为![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(一),在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置得到图(二),点
的位置得到图(二),点![]() 为棱
为棱![]() 上的动点.
上的动点.

(1)当![]() 在何处时,平面
在何处时,平面![]() 平面
平面![]() ,并证明;
,并证明;
(2)若![]() ,
,![]() ,证明:点
,证明:点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离,并求出该距离.
的距离,并求出该距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,设点![]() ,
,![]() ,
,![]() (其中
(其中![]() 表示a、b中的较大数)为
表示a、b中的较大数)为![]() 、
、![]() 两点的“切比雪夫距离”.
两点的“切比雪夫距离”.
(1)若![]() ,Q为直线
,Q为直线![]() 上动点,求P、Q两点“切比雪夫距离”的最小值;
上动点,求P、Q两点“切比雪夫距离”的最小值;
(2)定点![]() ,动点
,动点![]() 满足
满足![]()
![]() ,请求出P点所在的曲线所围成图形的面积.
,请求出P点所在的曲线所围成图形的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四面体ABCD中,DA=DB=DC=![]() 且DA、DB、DC两两互相垂直,点
且DA、DB、DC两两互相垂直,点![]() 是△ABC的中心.
是△ABC的中心.

(1)求直线DA与平面ABC所成角的大小(用反三角函数表示);
(2)过![]() 作OE⊥AD,垂足为E,求ΔDEO绕直线DO旋转一周所形成的几何体的体积;
作OE⊥AD,垂足为E,求ΔDEO绕直线DO旋转一周所形成的几何体的体积;
(3)将△DAO绕直线DO旋转一周,则在旋转过程中,直线DA与直线BC所成角记为![]() ,求
,求![]() 的取值范图.
的取值范图.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的焦距为2,左右焦点分别为
的焦距为2,左右焦点分别为![]() ,
,![]() ,以原点O为圆心,以椭圆C的半短轴长为半径的圆与直线
,以原点O为圆心,以椭圆C的半短轴长为半径的圆与直线![]() 相切.
相切.
![]() Ⅰ
Ⅰ![]() 求椭圆C的方程;
求椭圆C的方程;
![]() Ⅱ
Ⅱ![]() 设不过原点的直线l:
设不过原点的直线l:![]() 与椭圆C交于A,B两点.
与椭圆C交于A,B两点.
![]() 若直线
若直线![]() 与
与![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,且
,且![]() ,求证:直线l过定点,并求出该定点的坐标;
,求证:直线l过定点,并求出该定点的坐标;
![]() 若直线l的斜率是直线OA,OB斜率的等比中项,求
若直线l的斜率是直线OA,OB斜率的等比中项,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com