
【题目】已知数列![]() 满足
满足![]() ,对每个正整数
,对每个正整数![]() ,有
,有![]() 或
或![]() .如这个数列可以为1,2,4,6,10….
.如这个数列可以为1,2,4,6,10….
(1)若某一项![]() 为奇数,且不为3的倍数,证明:
为奇数,且不为3的倍数,证明:![]() ;
;
(2)证明: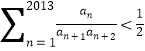 ;
;
(3)若在![]() 的前2015项中,恰有t个项为奇数,求t的最大值.
的前2015项中,恰有t个项为奇数,求t的最大值.
【答案】(1)见解析;(2)见解析;(3)1343
【解析】
(1)由am不为偶数,知![]() .
.
于是,![]() .
.
假如![]() ,则
,则![]() 为3的倍数,与已知条件矛盾.
为3的倍数,与已知条件矛盾.
从而,只能是![]() .
.
故![]() .
.
(2)由递推关系,易知数列![]() 是单调递增的.
是单调递增的.
因此,当![]() 时,
时,![]() .
.
从而,![]() ,即
,即![]() .
.
由此,![]() .
.
故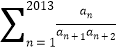
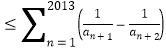
![]()
(3)一方面,数列![]() 的任意相邻三项至多有两个奇数.
的任意相邻三项至多有两个奇数.
事实上,假如![]() 均为奇数,由
均为奇数,由![]() 均为偶数,故根据递推关系知
均为偶数,故根据递推关系知![]() 为偶数,矛盾.
为偶数,矛盾.
因此,在![]() 这671组数中,每组至多含两个奇数.
这671组数中,每组至多含两个奇数.
再考虑到![]() 为奇数,
为奇数,![]() 为偶数,故至多有
为偶数,故至多有![]() 个奇数,即
个奇数,即![]() .
.
另一方面 ,当数列![]() 总满足
总满足![]() 时,注意到,
时,注意到,![]() 为奇数,
为奇数,![]() 为偶数,故对每个正整数k,由递推关系得
为偶数,故对每个正整数k,由递推关系得![]() 为奇数,
为奇数,![]() 为奇数,
为奇数,![]() 为偶数,此时,数列
为偶数,此时,数列![]() 的前2015项含有1343个奇数.
的前2015项含有1343个奇数.
综上,t的最大值1343.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C; ![]() =1(a>b>c)的左、右焦点分别为F1(﹣c,0)、F2(c,0),过原点O的直线(与x轴不重合)与椭圆C相交于D、Q两点,且|DF1|+|QF1|=4,P为椭圆C上的动点,△PF1F2的面积的最大值为
=1(a>b>c)的左、右焦点分别为F1(﹣c,0)、F2(c,0),过原点O的直线(与x轴不重合)与椭圆C相交于D、Q两点,且|DF1|+|QF1|=4,P为椭圆C上的动点,△PF1F2的面积的最大值为 ![]() .
. 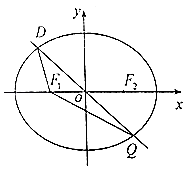
(1)求椭圆C的离心率;
(2)若A、B是椭圆C上关于x轴对称的任意两点,设点N(﹣4,0),连接NA与椭圆C相交于点E,直线BE与x轴相交于点M,试求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,设椭圆 ![]() =1(a>b>0)的左、右焦点分别为F1 , F2 , 右顶点为A,上顶点为B,离心率为e.椭圆上一点C满足:C在x轴上方,且CF1⊥x轴.
=1(a>b>0)的左、右焦点分别为F1 , F2 , 右顶点为A,上顶点为B,离心率为e.椭圆上一点C满足:C在x轴上方,且CF1⊥x轴.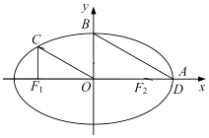
(1)若OC∥AB,求e的值;
(2)连结CF2并延长交椭圆于另一点D若 ![]() ≤e≤
≤e≤ ![]() ,求
,求 ![]() 的取值范围.
的取值范围.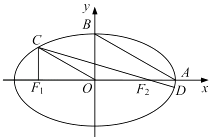
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log2(|x+1|+|x﹣1|﹣a)
(1)当a=3时,求函数f(x)的定义域;
(2)若不等式f(x)≥2的解集为R,求实数a的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的中心在原点,焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,且过点P
,且过点P![]() 。
。
(1)求椭圆的标准方程;
(2)已知斜率为1的直线l过椭圆的右焦点F交椭圆于A.B两点,求弦AB的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com