【题目】设函数
，
，已知
有三个互不相等的零点
，且
.
（Ⅰ）若
.(ⅰ)讨论的单调区间；(ⅱ)对任意的
，都有
成立，求
的取值范围；
（Ⅱ）若
且
，设函数在
，
处的切线分别为直线
，
，
是直线，的交点，求
的取值范围.
【答案】(I)(ⅰ)见解析，(ⅱ)
；(II)
【解析】
（Ⅰ）(ⅰ)先化简条件
得
，再求导数，根据导函数零点大小分类讨论，结合导函数符号确定单调性，(ⅱ)根据单调性确定函数最大值，再解不等式得结果，（Ⅱ）先化简，再求导数得切线斜率，根据点斜式得切线方程，求直线交点得
，再根据零点条件确定自变量取值范围，利用导数求其单调性，根据单调性确定取值范围.
(I) (ⅰ)
，
,
,
当
时，
在
，
单调递增，在
单调递减
当
时，在
，
单调递增，在
单调递减
(ⅱ)由(ⅰ)知当时，在
，
单调递增，在单调递减
当时，在
，
单调递增，在单调递减
不成立 ，综上
（II）令
则
或
，
令
，则
有两个零点为
且
又
对称轴为
，且
，设
的斜率分别为
与
的直线方程联立求得：
令
， 
在
恒成立，
在上单调递减， 而
科目：高中数学 来源： 题型：
【题目】在四棱锥
中，底面ABCD为菱形，
，侧面
为等腰直角三角形，
，
，点E为棱AD的中点．
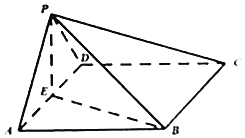
（1）求证：
平面ABCD；
（2）求直线AB与平面PBC所成角的正弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四棱锥P—ABCD中，PA⊥平面ABCD，∠ABC＝∠BAD＝90°，AD＝AP＝4，AB＝BC＝2，N为AD的中点．
（1）求异面直线PB与CD所成角的余弦值；
（2）点M在线段PC上且满足
，直线MN与平面PBC所成角的正弦值为
，求实数
的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知三棱柱ABC﹣A1B1C1的侧棱与底面边长都相等，A1在底面ABC内的射影为△ABC的中心，则AC1与底面ABC所成角的余弦值等于（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】2018年9月，台风“山竹”在我国多个省市登陆，造成直接经济损失达52亿元.某青年志愿者组织调查了某地区的50个农户在该次台风中造成的直接经济损失，将收集的数据分成五组：
，
，
，
，
（单位：元），得到如图所示的频率分布直方图.
（1）试根据频率分布直方图估计该地区每个农户的平均损失（同一组中的数据用该组区间的中点值代表）；
（2）台风后该青年志愿者与当地政府向社会发出倡议，为该地区的农户捐款帮扶，现从这50户并且损失超过4000元的农户中随机抽取2户进行重点帮扶，设抽出损失超过8000元的农户数为
，求的分布列和数学期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】[选修4-4：坐标系与参数方程]
在直角坐标系
中，曲线
的参数方程为
（
为参数，
），以坐标原点为极点，
轴的正半轴为极轴建立极坐标系，曲线
的极坐标方程为
.
（1）求的普通方程和极坐标方程；
（2）若与相交于
、
两点，且
，求
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
