练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    当a取2，3，5，10时，画出对数函数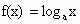的图象，由所画图象归纳：当底数a满足a＞1时，对数函数的图象上升的快慢与底数的大小有什么关系？当底数a满足0＜a＜1时，你又能发现什么规律？

    答案：略
    解析：

    当a取2，3，5，10时，画出对数函数的图象，观察图象可得到当底数a＞1时，对数函数的图象随底数增大，上升的越来越慢．

    当底数a满足0＜a＜1时，应该得到的结论是：对数函数的图象随底数的增大，下降得越来越快．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （2010•宿州三模）已知二次曲线
    x2
    4
    +
    y2
    m
    =1，则当m∈[-2，-1]    时，该曲线的离心率的取值范围是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•蓟县二模）已知函数f（x）=-
    1
    3
    x3+
    1
    2
    (2a+1)x2    -2ax+1，其中a为实数．
    （Ⅰ）当a≠
    1
    2
    时，求函数f（x）的极大值点和极小值点；
    （Ⅱ） 若对任意a∈（2，3）及x∈[1，3]时，恒有ta2-f（x）＞
    3
    2
    成立，求实数t的取值范围．
    （Ⅲ）已知g（x）=a2x2+ax+1，m（x）=
    4
    3
    x3-(a2+
    3
    2
    )x2    +（2a+5）x-3，h（x）=f（x）+m（x），设函数q（x）=
    g(x)，x≥0
    h(x)，x＜0.
    是否存在a，对任意给定的非零实数x1，存在惟一的非零实数x2（x2≠x1），使得q′（x2）=q′（x1）成立？若存在，求a的值；若不存，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源：数学教研室 题型：044

    当a取2，3，5，10时，画出对数函数的图象，由所画图象归纳：当底数a满足a＞1时，对数函数的图象上升的快慢与底数的大小有什么关系？当底数a满足0＜a＜1时，你又能发现什么规律？

    查看答案和解析>>

    科目：高中数学 来源：模拟题 题型：解答题

    已知数列{an}满足：a1=a，an+1=1+，不难发现，当a取不同的值时，可以得到不同的数列，例如，当a=1时，得到无穷数列：1，2，，，…；当a=-时，得到有穷数列：-，-1，0。
    （1）当a为何值时，a4=0；
    （2）设数列{bn}满足：b1=-1，bn+1=（n∈N*）求证：a取数列{bn}中的任何一个数，都可得到一个有穷数列{an}；
    （3）若对任意n∈N*且n≥5，都有＜an＜2成立，试求a 的取值范围。

    查看答案和解析>>

    同步练习册答案