
【题目】已知函数f(x)=A cos(ωx+φ)(A>0,ω>0)的部分图象如图所示,下面结论错误的是( )

A. 函数f(x)的最小正周期为![]()
B. 函数f(x)的图象可由g(x)=Acos ωx的图象向右平移![]() 个单位长度得到
个单位长度得到
C. 函数f(x)的图象关于直线x=![]() 对称
对称
D. 函数f(x)在区间![]() 上单调递增
上单调递增
【答案】D
【解析】∵由题意可知,此函数的周期T=2(![]() ﹣
﹣![]() )
)![]() ,
,
∴解得:ω=3,可得:f(x)=Acos(3x+φ).
又∵由题图可知f(![]() )=Acos(3×
)=Acos(3×![]() +φ)=Acos(φ﹣
+φ)=Acos(φ﹣![]() π)=0,
π)=0,
∴利用五点作图法可得:φ﹣![]() π=
π=![]() ,解得:φ=
,解得:φ=![]() ,
,
∴f(x)=Acos(3x+![]() ).
).
∴令3x+![]() =kπ,k∈Z,可解得函数的对称轴方程为:x=
=kπ,k∈Z,可解得函数的对称轴方程为:x=![]() ﹣
﹣![]() ,k∈Z,
,k∈Z,
令2kπ﹣π≤3x+![]() ≤2kπ,k∈Z,可解得:
≤2kπ,k∈Z,可解得: ![]() kπ﹣
kπ﹣![]() ≤x≤
≤x≤![]() kπ﹣
kπ﹣![]() ,k∈Z,
,k∈Z,
故函数的单调递增区间为:[![]() kπ﹣
kπ﹣![]() ,
, ![]() kπ﹣
kπ﹣![]() ],k∈Z.
],k∈Z.
∴对于A,函数f(x)的最小周期为![]() ,故A正确;
,故A正确;
对于B,因为g(x)=Acos3x的图象向右平移![]() 个单位得到y=Acos[3(x﹣
个单位得到y=Acos[3(x﹣![]() )]=Acos(3x﹣
)]=Acos(3x﹣![]() )=Acos(3x﹣
)=Acos(3x﹣![]() )=Acos(3x+
)=Acos(3x+![]() )=f(x),故B正确;
)=f(x),故B正确;
对于C,因为函数的对称轴方程为:x=![]() ﹣
﹣![]() ,k∈Z,令k=2,可得函数f(x)的图象关于直线x=
,k∈Z,令k=2,可得函数f(x)的图象关于直线x=![]() 对称,故C正确;
对称,故C正确;
对于D,因为函数的单调递增区间为:[![]() kπ﹣
kπ﹣![]() ,
, ![]() kπ﹣
kπ﹣![]() ],k∈Z,令k=2,可得函数单调递增区间为:[
],k∈Z,令k=2,可得函数单调递增区间为:[![]() ,
, ![]() ],故函数f(x)在区间(
],故函数f(x)在区间(![]() ,
, ![]() )上不单调递增,故D错误.
)上不单调递增,故D错误.
故选:D.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,其中一个焦点与抛物线
的中心在原点,其中一个焦点与抛物线![]() 的焦点重合,点
的焦点重合,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)设椭圆的左右焦点分别为![]() ,过
,过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,若
两点,若![]() 的面积为
的面积为![]() ,求以
,求以![]() 为圆心且与直线
为圆心且与直线![]() 相切的圆的方程.
相切的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两地相距![]() 海里,某货轮匀速行驶从甲地运输货物到乙地,运输成本包括燃料费用和其他费用.已知该货轮每小时的燃料费与其速度的平方成正比,比例系数为
海里,某货轮匀速行驶从甲地运输货物到乙地,运输成本包括燃料费用和其他费用.已知该货轮每小时的燃料费与其速度的平方成正比,比例系数为![]() ,其他费用为每小时
,其他费用为每小时![]() 元,且该货轮的最大航行速度为
元,且该货轮的最大航行速度为![]() 海里/小时.
海里/小时.
(![]() )请将该货轮从甲地到乙地的运输成本
)请将该货轮从甲地到乙地的运输成本![]() 表示为航行速度
表示为航行速度![]() (海里/小时)的函数.
(海里/小时)的函数.
(![]() )要使从甲地到乙地的运输成本最少,该货轮应以多大的航行速度行驶?
)要使从甲地到乙地的运输成本最少,该货轮应以多大的航行速度行驶?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果双曲线的离心率e=![]() ,则称此双曲线为黄金双曲线.有以下几个命题:①双曲线
,则称此双曲线为黄金双曲线.有以下几个命题:①双曲线![]() 是黄金双曲线;②双曲线
是黄金双曲线;②双曲线![]() 是黄金双曲线;③在双曲线
是黄金双曲线;③在双曲线![]() (a>0,b>0)中,F1为左焦点,A2为右顶点,B1(0,b),若∠F1B1A2=90°,则该双曲线是黄金双曲线;④在双曲线
(a>0,b>0)中,F1为左焦点,A2为右顶点,B1(0,b),若∠F1B1A2=90°,则该双曲线是黄金双曲线;④在双曲线![]() (a>0,b>0)中,过右焦点F2作实轴的垂线交双曲线于M,N两点,O为坐标原点,若∠MON=120°,则该双曲线是黄金双曲线.其中正确命题的序号为________.
(a>0,b>0)中,过右焦点F2作实轴的垂线交双曲线于M,N两点,O为坐标原点,若∠MON=120°,则该双曲线是黄金双曲线.其中正确命题的序号为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=sin 2x+![]() cos 2x图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将图象上所有点向右平移
cos 2x图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将图象上所有点向右平移![]() 个单位长度,得到函数g(x)的图象,则g(x)图象的一条对称轴方程是( )
个单位长度,得到函数g(x)的图象,则g(x)图象的一条对称轴方程是( )
A. x=-![]() B. x=
B. x=![]()
C. x=![]() D. x=
D. x=![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系中,曲线![]() :
: ![]() 经过伸缩变换
经过伸缩变换![]() 后得到曲线
后得到曲线![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求出曲线![]() 、
、![]() 的参数方程;
的参数方程;
(Ⅱ)若![]() 、
、![]() 分别是曲线
分别是曲线![]() 、
、![]() 上的动点,求
上的动点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
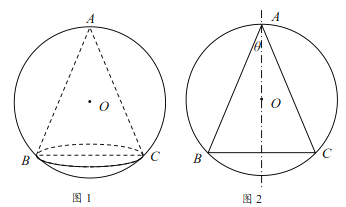
【题目】某艺术品公司欲生产一款迎新春工艺礼品,该礼品是由玻璃球面和该球的内接圆锥组成,圆锥的侧面用于艺术装饰,如图1.为了便于设计,可将该礼品看成是由圆![]() 及其内接等腰三角形
及其内接等腰三角形![]() 绕底边
绕底边![]() 上的高所在直线
上的高所在直线![]() 旋转180°而成,如图2.已知圆
旋转180°而成,如图2.已知圆![]() 的半径为
的半径为![]() ,设
,设![]() ,圆锥的侧面积为
,圆锥的侧面积为![]() .
.
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)为了达到最佳观赏效果,要求圆锥的侧面积![]() 最大.求
最大.求![]() 取得最大值时腰
取得最大值时腰![]() 的长度.
的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com