
分析 (1)通过将点A代入函数f(x)=3ax+b可得a+b=1,进而有an=log3f(n)=a(n-1)+1,利用数列{an}的第1项,第2项,第5项成等比数列,计算可得a=2,从而可得结论;
(2)通过an=2n-1可得bn=$\frac{2n-1}{{2}^{n}}$,采用错位相减法即得Tn=3-$\frac{2n+3}{{2}^{n}}$,利用作商法易得$\frac{2n+3}{{2}^{n}}$随着n的增大而减小,从而Tn随着n的增大而增大,通过$\underset{lim}{n→∞}$(3-$\frac{2n+3}{{2}^{n}}$)=3,即得结论.
解答 解:(1)∵函数f(x)=3ax+b的图象经过点A(1,3),
∴f(1)=3a+b=3,∴a+b=1,
∴an=log3f(n)=an+b=a(n-1)+1,
∵数列{an}的第1项,第2项,第5项成等比数列,
∴a1•a5=(a2)2,
即1•(4a+1)=(a+1)2,
解得a=2或0(递增数列,故舍),
∴数列{an}的通项公式an=2n-1;
(2)∵an=2n-1,
∴bn=$\frac{a_n}{2^n}$=$\frac{2n-1}{{2}^{n}}$,
∴Tn=b1+b2+…+bn
=$\frac{1}{{2}^{1}}$+3×$\frac{1}{{2}^{2}}$+5×$\frac{1}{{2}^{3}}$+…+(2n-1)×$\frac{1}{{2}^{n}}$,
∴2Tn=$\frac{1}{{2}^{0}}$+3×$\frac{1}{{2}^{1}}$+5×$\frac{1}{{2}^{2}}$+…+(2n-1)×$\frac{1}{{2}^{n-1}}$,
两式相减得:Tn=$\frac{1}{{2}^{0}}$+2($\frac{1}{{2}^{1}}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n-1}}$)-(2n-1)×$\frac{1}{{2}^{n}}$
=1+2×$\frac{\frac{1}{2}(1-\frac{1}{{2}^{n-1}})}{1-\frac{1}{2}}$-(2n-1)×$\frac{1}{{2}^{n}}$
=1+2-$\frac{4}{{2}^{n}}$-$\frac{2n-1}{{2}^{n}}$
=3-$\frac{2n+3}{{2}^{n}}$,
设f(n)=$\frac{2n+3}{{2}^{n}}$,
∵$\frac{f(n+1)}{f(n)}$=$\frac{\frac{2n+5}{{2}^{n+1}}}{\frac{2n+3}{{2}^{n}}}$=$\frac{2n+5}{2(2n+3)}$=$\frac{1}{2}$+$\frac{1}{2n+3}$≤$\frac{1}{2}$+$\frac{1}{5}$<1,
∴f(n)随着n的增大而减小,
从而Tn随着n的增大而增大,
∴$\underset{lim}{n→∞}$Tn=$\underset{lim}{n→∞}$(3-$\frac{2n+3}{{2}^{n}}$)=3,
∵Tn<m(m∈Z)对n∈N*恒成立,
∴m的最小值为3.
点评 本题是一道关于数列的综合题,考查运算求解能力,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
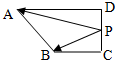 在直角梯形ABCD中,∠ADC=90°,BC=CD=1,AD=2,P是线段CD上一动点,则$|\overrightarrow{PA}+3\overrightarrow{PB}|$的取值范围是[5,$\sqrt{34}$].
在直角梯形ABCD中,∠ADC=90°,BC=CD=1,AD=2,P是线段CD上一动点,则$|\overrightarrow{PA}+3\overrightarrow{PB}|$的取值范围是[5,$\sqrt{34}$].查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com