
给出集合A={-2,-1,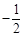 ,
,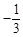 ,
,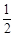 ,1,2,3}。已知a∈A,使得幂函数
,1,2,3}。已知a∈A,使得幂函数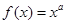 为奇函数,指数函数
为奇函数,指数函数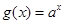 在区间(0,+∞)上为增函数。
在区间(0,+∞)上为增函数。
(1)试写出所有符合条件的a,说明理由;
(2)判断f(x)在(0,+∞)的单调性,并证明;
(3)解方程:f[g(x)]=g[f (x)]。
(1)a=3
(2)f(x)=x3在(0,+∞)上为增函数
(3)x1=0,x2=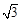 ,x3=
,x3=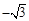
【解析】解:(1)指数函数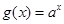 在区间(0,+∞)上为增函数,∴a>1,∴a只可能为2或3。而当a=2时,幂函数f(x)=x2为偶函数,只有当a=3时,幂函数f(x)=x3为奇函数故a=3…3分
在区间(0,+∞)上为增函数,∴a>1,∴a只可能为2或3。而当a=2时,幂函数f(x)=x2为偶函数,只有当a=3时,幂函数f(x)=x3为奇函数故a=3…3分
(2)f(x)=x3在(0,+∞)上为增函数。
证明:在(0,+∞)上任取x1,x2,x1<x2,
f(x1)-f(x2)= =
=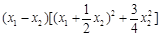 ,
,
∵x1<x2,∴x1-x2<0,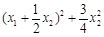 >0,∴f(x1)-f(x2)>0,∴f(x1)>f(x2)。
>0,∴f(x1)-f(x2)>0,∴f(x1)>f(x2)。
∴f(x)=x3在(0,+∞)上为增函数。 …8分
(3)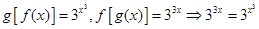 ....10分
....10分
根据指数函数的性质,得3x=x3,∴x1=0,x2=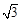 ,x3=
,x3=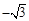 。 …12分
。 …12分


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 ,
, ,
, ,1,2,3}.已知a∈A,使得幂函数f(x)=xa为奇函数;指数函数g(x)=ax在区间(0,+∞)上为增函数.
,1,2,3}.已知a∈A,使得幂函数f(x)=xa为奇函数;指数函数g(x)=ax在区间(0,+∞)上为增函数.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com