[题目]已知二项式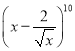的展开式.(1)求展开式中含项的系数,(2)如果第项和第项的二项式系数相等.求的值．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】已知二项式的展开式.

(1)求展开式中含项的系数；

(2)如果第项和第项的二项式系数相等，求的值．

【答案】（1）；（2）1

【解析】试题分析：（1）写出二项展开式的通项公式，当的指数是时，可得到关于方程，解方程可得的值，从而可得展开式中含项的系数；（2）根据上一问写出的通项公式，利用第项和第项的二项式系数相等，可得到一个关于的方程，解方程即可得结果.

试题解析：(1)设第k＋1项为Tk＋1＝

令10－k＝4，解得k＝4，

故展开式中含x4项的系数为3 360.

(2)∵第3r项的二项式系数为，第r＋2项的二项式系数为，

∵ ＝，故3r－1＝r＋1或3r－1＋r＋1＝10，

解得r＝1或r＝2.5(不合题意，舍去)，∴r＝1.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知函数f（x），g（x）满足关系g（x）=f（x）f（x+α），其中α是常数．

（1）设f（x）=cosx+sinx，，求g（x）的解析式；

（2）设计一个函数f（x）及一个α的值，使得；

（3）当f（x）=|sinx|+cosx，时，存在x1，x2∈R，对任意x∈R，g（x1）≤g（x）≤g（x2）恒成立，求|x1-x2|的最小值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】给定下列四个命题：

若一个平面内的两条直线与另一个平面都平行，那么这两个平面相互平行；

若一个平面经过另一个平面的垂线，那么这两个平面相互垂直；

垂直于同一直线的两条直线相互平行；

若两个平面垂直，那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直．

其中，为真命题的是　　

A. 和 B. 和 C. 和 D. 和

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，在三棱台ABC﹣DEF中，已知平面BCFE⊥平面ABC，∠ACB=90°，BE=EF=FC=1，BC=2，AC=3，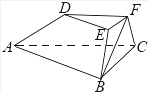

（1）求证：EF⊥平面ACFD；
（2）求二面角B﹣AD﹣F的余弦值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】若函数与的图像有两个不同交点，则实数的取值范围是（）

A. B. C. D.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某高科技企业生产产品A和产品B需要甲、乙两种新型材料．生产一件产品A需要甲材料1.5kg，乙材料1kg，用5个工时；生产一件产品B需要甲材料0.5kg，乙材料0.3kg，用3个工时，生产一件产品A的利润为2100元，生产一件产品B的利润为900元．该企业现有甲材料150kg，乙材料90kg，则在不超过600个工时的条件下，生产产品A、产品B的利润之和的最大值为元．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】椭圆离心率为，，是椭圆的左、右焦点，以为圆心，为半径的圆和以为圆心、为半径的圆的交点在椭圆上.