
| A. | [-1,1+2$\sqrt{2}$] | B. | [1-2$\sqrt{2}$,1+2$\sqrt{2}$] | C. | [1-2$\sqrt{2}$,3] | D. | [1-$\sqrt{2}$,3] |
分析 曲线表示以(2,3)为圆心、半径等于2的半圆,当半圆和直线y=x+b相切时,求得b的值;当直线y=x+b经过点(0,3)时,求得b的值,数形结合求得b的范围.
解答 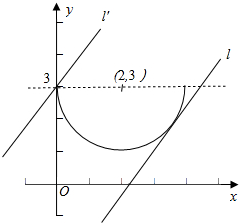 解:曲线x2-4x+y2-6y+9=0,即(x-2)2+(y-3)2 =4 (y≤3),
解:曲线x2-4x+y2-6y+9=0,即(x-2)2+(y-3)2 =4 (y≤3),
表示以(2,3)为圆心、半径等于2的半圆,
如图所示:当半圆和直线y=x+b相切时,由$\frac{|2-3+b|}{\sqrt{2}}$=2,
求得b=1-2$\sqrt{2}$,或b=1+2$\sqrt{2}$(舍去).
当直线y=x+b经过点(0,3)时,求得b=3.
综上可得,b的取值范围是[1-2$\sqrt{2}$,3],
故选:C.
点评 本题主要考查圆的标准方程,直线和圆的位置关系,体现了数形结合的数学思想,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | -28 | B. | -8 | C. | -4 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9\sqrt{2}}{2}$ | B. | $\frac{9\sqrt{2}}{4}$ | C. | $\frac{9\sqrt{2}}{6}$ | D. | 8$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
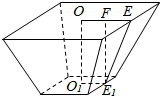 已知正四棱台高是12cm,两底面边长之差为10cm,全面积为512cm2.
已知正四棱台高是12cm,两底面边长之差为10cm,全面积为512cm2. 查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com