
【题目】已知函数![]() (
(![]() 且
且![]() )的零点是
)的零点是![]() .
.
(1)设曲线![]() 在零点处的切线斜率分别为
在零点处的切线斜率分别为![]() ,判断
,判断![]() 的单调性;
的单调性;
(2)设![]() 是
是![]() 的极值点,求证:
的极值点,求证:![]() .
.
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为![]() (θ为参数),以原点为极点,x轴非负半轴为极轴,建立极坐标系,曲线C2的极坐标方程为
(θ为参数),以原点为极点,x轴非负半轴为极轴,建立极坐标系,曲线C2的极坐标方程为![]() .
.
(1)求曲线C1的极坐标方程以及曲线C2的直角坐标方程;
(2)若直线l:y=kx与曲线C1、曲线C2在第一象限交于P、Q,且|OQ|=|PQ|,点M的直角坐标为(1,0),求△PMQ的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中“勾股容方”问题:“今有勾五步,股十二步,问勾中容方几何?”魏晋时期数学家刘徽在其《九章算术注》中利用出入相补原理给出了这个问题的一般解法:如图1,用对角线将长和宽分别为![]() 和
和![]() 的矩形分成两个直角三角形,每个直角三角形再分成一个内接正方形(黄)和两个小直角三角形(朱、青).将三种颜色的图形进行重组,得到如图2所示的矩形.该矩形长为
的矩形分成两个直角三角形,每个直角三角形再分成一个内接正方形(黄)和两个小直角三角形(朱、青).将三种颜色的图形进行重组,得到如图2所示的矩形.该矩形长为![]() ,宽为内接正方形的边长
,宽为内接正方形的边长![]() .由刘徽构造的图形还可以得到许多重要的结论,如图3.设
.由刘徽构造的图形还可以得到许多重要的结论,如图3.设![]() 为斜边
为斜边![]() 的中点,作直角三角形
的中点,作直角三角形![]() 的内接正方形对角线
的内接正方形对角线![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,则下列推理正确的是( )
,则下列推理正确的是( )
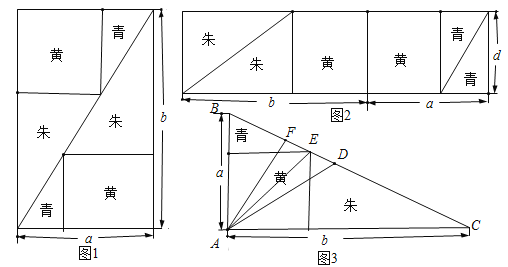
①由图1和图2面积相等得![]() ;
;
②由![]() 可得
可得![]() ;
;
③由![]() 可得
可得 ;
;
④由![]() 可得
可得![]() .
.
A.①②③④B.①②④C.②③④D.①③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的普通方程为:
的普通方程为:![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,正方形
,正方形![]() 的顶点都在
的顶点都在![]() 上,且
上,且![]() 逆时针依次排列,点
逆时针依次排列,点![]() 的极坐标为
的极坐标为![]()
(1)写出曲线![]() 的参数方程,及点
的参数方程,及点![]() 的直角坐标;
的直角坐标;
(2)设![]() 为椭圆
为椭圆![]() 上的任意一点,求:
上的任意一点,求:![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十八大以来,党中央提出要在2020年实现全面脱贫,为了实现这一目标,国家对“新农合”(新型农村合作医疗)推出了新政,各级财政提高了对“新农合”的补助标准.提高了各项报销的比例,其中门诊报销比例如下:
表1:新农合门诊报销比例
医院类别 | 村卫生室 | 镇卫生院 | 二甲医院 | 三甲医院 |
门诊报销比例 | 60% | 40% | 30% | 20% |
根据以往的数据统计,李村一个结算年度门诊就诊人次情况如下:
表2:李村一个结算年度门诊就诊情况统计表
医院类别 | 村卫生室 | 镇卫生院 | 二甲医院 | 三甲医院 |
一个结算年度内各门诊就诊人次占李村总就诊人次的比例 | 70% | 10% | 15% | 5% |
如果一个结算年度每人次到村卫生室、镇卫生院、二甲医院、三甲医院门诊平均费用分别为50元、100元、200元、500元.若李村一个结算年度内去门诊就诊人次为2000人次.
(Ⅰ)李村在这个结算年度内去三甲医院门诊就诊的人次中,60岁以上的人次占了80%,从去三甲医院门诊就诊的人次中任选2人次,恰好2人次都是60岁以上人次的概率是多少?
(Ⅱ)如果将李村这个结算年度内门诊就诊人次占全村总就诊人次的比例视为概率,求李村这个结算年度每人次用于门诊实付费用(报销后个人应承担部分)![]() 的分布列与期望.
的分布列与期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设点![]() 是抛物线
是抛物线![]() 的焦点,直线
的焦点,直线![]() 与抛物线
与抛物线![]() 相切于点
相切于点![]() (点
(点![]() 位于第一象限),并与抛物线
位于第一象限),并与抛物线![]() 的准线相交于点
的准线相交于点![]() .过点
.过点![]() 且与直线
且与直线![]() 垂直的直线
垂直的直线![]() 交抛物线
交抛物线![]() 于另一点
于另一点![]() ,交
,交![]() 轴于点
轴于点![]() ,连结
,连结![]() .
.
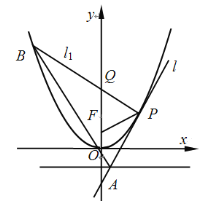
(1)证明:![]() 为等腰三角形;
为等腰三角形;
(2)求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论中正确的个数是( )
①在![]() 中,“
中,“![]() ”是“
”是“![]() ”的必要不充分条件;
”的必要不充分条件;
②若![]() ,
,![]() 的最小值为2;
的最小值为2;
③夹在圆柱的两个平行截面间的几何体是圆柱;
④数列![]() 的通项公式为
的通项公式为![]() ,则数列的前
,则数列的前![]() 项和
项和![]() .( )
.( )
A.0B.1C.2D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com