
【题目】已知A是圆O:x2+y2=4上一动点,过点A作AB⊥x轴,垂足为B,动点D满足![]() .
.
(1)求动点D的轨迹C的方程;
(2)垂直于x轴的直线M交轨迹C于M、N两点,点P(3,0),直线PM与轨迹C的另一个交点为Q.问:直线NQ是否过一定点?若过定点,求出该定点的坐标;若不过定点,请说明理由.
【答案】(1)![]() ;(2)直线NQ恒过定点
;(2)直线NQ恒过定点![]()
【解析】
(1)设![]() ,用
,用![]() 表示出
表示出![]() 点坐标,代入圆
点坐标,代入圆![]() 方程化简即可得
方程化简即可得![]() 的轨迹方程;
的轨迹方程;
(2)设直线![]() 斜率为
斜率为![]() ,根据根与系数的关系得出
,根据根与系数的关系得出![]() 的坐标关系,利用两点式表示出直线
的坐标关系,利用两点式表示出直线![]() 的方程,化简即可得出结论.
的方程,化简即可得出结论.
(1)设D(x,y),∵![]() ,∴A(x,
,∴A(x,![]() ),
),
代入圆O的方程可得:x2![]() 4,即
4,即![]() 1.
1.
∴动点D的轨迹C的方程是:![]() 1.
1.
(2)设直线PM的方程为y=k(x﹣3),
联立方程组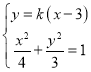 ,消元得:(3+4k2)x2﹣24k2x+36k2﹣12=0,
,消元得:(3+4k2)x2﹣24k2x+36k2﹣12=0,
∴△=576k4﹣4(3+4k2)(36k2﹣12)![]() 0,解得:k2
0,解得:k2![]() .
.
设M(x1,y1),Q(x2,y2),则N(x1,﹣y1),
由根与系数的关系可得:x1+x2![]() ,x1x2
,x1x2![]() ,
,
直线NQ的方程为:![]() ,
,
即(x2﹣x1)y﹣(y1+y2)x+x2y1+x1y2=0,
∵y1+y2=k(x1﹣3)+k(x2﹣3)=k(x1+x2)﹣6![]() 6
6![]() ,
,
x2y1+x1y2=x2k(x1﹣3)+x1k(x2﹣3)=2kx1x2﹣3k(x1+x2)=2k![]() 3k
3k![]() ,
,
∴直线NQ方程为:(x2﹣x1)![]()
![]() 0,即(x2﹣x1)
0,即(x2﹣x1)![]() =0,
=0,
∴直线NQ恒过定点(![]() ,0).
,0).


科目:高中数学 来源: 题型:
【题目】我国古代数学家提出的“中国剩余定理”又称“孙子定理”,它在世界数学史上具有光辉的一页,堪称数学史上名垂百世的成就,而且一直启发和指引着历代数学家们.定理涉及的是数的整除问题,其数学思想在近代数学、当代密码学研究及日常生活都有着广泛应用,为世界数学的发展做出了巨大贡献,现有这样一个整除问题:将1到2019这2019个整数中能被5除余1且被7除余2的数按从小到大的顺序排成一列,构成数列![]() ,那么此数列的项数为( )
,那么此数列的项数为( )
A.56B.57C.58D.59
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新高考方案规定,普通高中学业水平考试分为合格性考试(合格考)和选择性考试(选择考).其中“选择考”成绩将计入高考总成绩,即“选择考”成绩根据学生考试时的原始卷面分数,由高到低进行排序,评定为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五个等级.某试点高中2018年参加“选择考”总人数是2016年参加“选择考”总人数的2倍,为了更好地分析该校学生“选择考”的水平情况,统计了该校2016年和2018年“选择考”成绩等级结果,得到如下图表:
五个等级.某试点高中2018年参加“选择考”总人数是2016年参加“选择考”总人数的2倍,为了更好地分析该校学生“选择考”的水平情况,统计了该校2016年和2018年“选择考”成绩等级结果,得到如下图表:
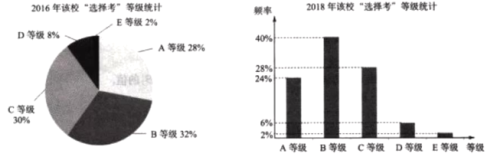
针对该校“选择考”情况,2018年与2016年比较,下列说法正确的是( )
A. 获得A等级的人数减少了B. 获得B等级的人数增加了1.5倍
C. 获得D等级的人数减少了一半D. 获得E等级的人数相同
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点F是椭圆C:![]() 1(a>b>0)的一个焦点,点D是椭圆上的一个动点,且|FD|∈[1,3].
1(a>b>0)的一个焦点,点D是椭圆上的一个动点,且|FD|∈[1,3].
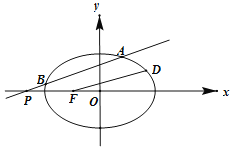
(Ⅰ)求椭圆的标准方程;
(Ⅱ)过点P(﹣4,0)作直线交椭圆C于A,B两点,求△AOB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中有一分鹿问题:“今有大夫、不更、簪袅、上造、公士,凡五人,共猎得五鹿.欲以爵次分之,问各得几何.”在这个问题中,大夫、不更、簪袅、上造、公士是古代五个不同爵次的官员,现皇帝将大夫、不更、簪枭、上造、公士这5人分成两组(一组2人,一组3人),派去两地执行公务,则大夫、不更恰好在同一组的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学棋艺协会定期举办“以棋会友”的竞赛活动,分别包括“中国象棋”、“围棋”、“五子棋”、“国际象棋”四种比赛,每位协会会员必须参加其中的两种棋类比赛,且各队员之间参加比赛相互独立;已知甲同学必选“中国象棋”,不选“国际象棋”,乙、丙两位同学从四种比赛中任选两种参与.
(1)求甲、乙同时参加围棋比赛的概率;
(2)记甲、乙、丙三人中选择“中国象棋”比赛的人数为![]() ,求
,求![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,上、下顶点分别为
,上、下顶点分别为![]() ,若
,若![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点在椭圆
的对称点在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程与离心率;
的方程与离心率;
(2)过点![]() 做直线
做直线![]() 与椭圆
与椭圆![]() 相交于两个不同的点
相交于两个不同的点![]() ;若
;若![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列叙述错误的是( ).
A.若事件![]() 发生的概率为
发生的概率为![]() ,则
,则![]()
B.互斥事件不一定是对立事件,但是对立事件一定是互斥事件
C.某事件发生的概率是随着试验次数的变化而变化的
D.5张奖券中有一张有奖,甲先抽,乙后抽,则乙与甲中奖的可能性相同
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com