
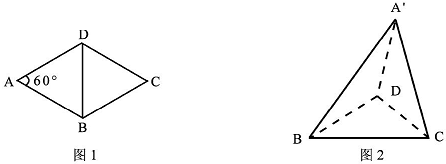 (2013•凉山州二模)图1是边长为1的菱形,∠DAB=60°,现沿BD将△ABD翻折起,得四面体A′-BDC(图2),若二面角A′-BD-C的平面角为α(0<a<π),给出以下四个命题:
(2013•凉山州二模)图1是边长为1的菱形,∠DAB=60°,现沿BD将△ABD翻折起,得四面体A′-BDC(图2),若二面角A′-BD-C的平面角为α(0<a<π),给出以下四个命题:| 3 |
| 1 |
| 3 |
| 5π |
| 3 |
| 3 |
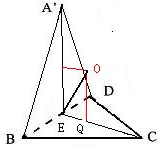
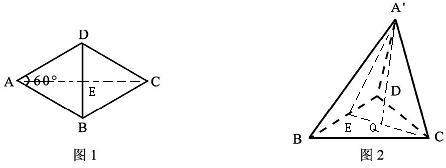 解:①取BD的中点E,连结A'E,EC,如图,则A'E⊥BD,EC⊥BD,∴BD⊥平面A'EC,A'C?平面A'EC,
解:①取BD的中点E,连结A'E,EC,如图,则A'E⊥BD,EC⊥BD,∴BD⊥平面A'EC,A'C?平面A'EC,| 3 |
| 3 |
| EQ |
| A′E |
| EQ |
| CE |
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 2 |
| 1 |
| 3 |
| ||
| 3 |
| 5 |
| 12 |
| 5π |
| 3 |


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com