
【题目】如图1,△ABC是等腰直角三角形∠CAB=90°,AC=2a,E,F分别为AC,BC的中点,沿EF将△CEF折起,得到如图2所示的四棱锥C′﹣ABFE
(1)求证:AB⊥平面AEC′;
(2)当四棱锥C′﹣ABFE体积取最大值时,
①若G为BC′中点,求异面直线GF与AC′所成角;
②在C′﹣ABFE中AE交BF于C,求二面角A﹣CC′﹣B的余弦值.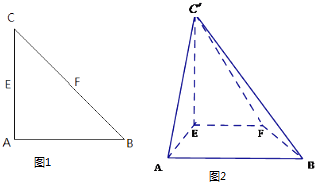
【答案】
(1)解:证明:因为△ABC 是等腰直角三角形,∠CAB=90°,E,F 分别为AC,BC 的中点,
所以EF⊥AE,EF⊥C'E.
又因为AE∩C'E=E,所以EF⊥平面AEC'.
由于EF∥AB,所以有AB⊥平面AEC'.
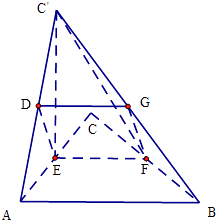
(2)解:①取AC'中点D,连接DE,EF,FG,GD,
由于GD 为△ABC'中位线,以及EF 为△ABC 中位线,
所以四边形DEFG 为平行四边形.
直线GF 与AC'所成角就是DE 与AC'所成角.
所以四棱锥C'﹣ABFE 体积取最大值时,C'E 垂直于底面ABFE.
此时△AEC'为等腰直角三角形,
ED 为中线,所以直线ED⊥AC'.
又因为ED∥GF,所以直线GF 与AC'所成角为 ![]() .
.
② 因为四棱锥C'﹣ABFE 体积取最大值,
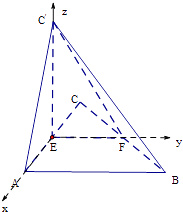
分别以EA、EF、EC'所在直线为x 轴、y 轴、z 轴,建立空间直角坐标系如图,
则C'(0,0,a),B(a,2a,0),F(0,a,0),C'B(a,2a,﹣a),C'F(0,a,﹣a).
设平面C'BF 的一个法向量为 ![]() =(x,y,z),
=(x,y,z),
由 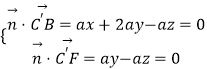 得,取y=1,得
得,取y=1,得 ![]() =(﹣1,1,1).
=(﹣1,1,1).
平面C'AE 的一个法向量 ![]() =(0,1,0).
=(0,1,0).
所以cos< ![]() >=
>= ![]() =
= ![]() ,
,
故平面C'AE与平面C'BF的平面角的夹角的余弦值为 ![]() .
.
【解析】(1)推导出EF⊥AE,EF⊥C'E,从而EF⊥平面AEC',由此能证明AB⊥平面AEC'.(2)①取AC'中点D,连接DE,EF,FG,GD,推导出四边形DEFG 为平行四边形,直线GF 与AC'所成角就是DE 与AC'所成角,由此能求出直线GF 与AC'所成角.②分别以EA、EF、EC'所在直线为x 轴、y 轴、z 轴,建立空间直角坐标系,利用向量法能求出平面C'AE与平面C'BF的平面角的夹角的余弦值.


科目:高中数学 来源: 题型:
【题目】在等差数列{an}中,2a9=a12+13,a2=5,其前n项和为Sn .
(1)求数列{an}的通项公式;
(2)求数列{ ![]() }的前n项和Tn , 并证明Tn<
}的前n项和Tn , 并证明Tn< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,某镇有一块空地![]() ,其中
,其中![]() ,
, ![]() ,
, ![]() 。当地镇政府规划将这块空地改造成一个旅游景点,拟在中间挖一个人工湖
。当地镇政府规划将这块空地改造成一个旅游景点,拟在中间挖一个人工湖![]() ,其中
,其中![]() 都在边
都在边![]() 上,且
上,且![]() ,挖出的泥土堆放在
,挖出的泥土堆放在![]() 地带上形成假山,剩下的
地带上形成假山,剩下的![]() 地带开设儿童游乐场. 为安全起见,需在
地带开设儿童游乐场. 为安全起见,需在![]() 的周围安装防护网.
的周围安装防护网.
(1)当![]() 时,求防护网的总长度;
时,求防护网的总长度;
(2)若要求挖人工湖用地![]() 的面积是堆假山用地
的面积是堆假山用地![]() 的面积的
的面积的![]() 倍,试确定
倍,试确定![]() 的大小;
的大小;
(3)为节省投入资金,人工湖![]() 的面积要尽可能小,问如何设计施工方案,可使
的面积要尽可能小,问如何设计施工方案,可使![]() 的面积最小?最小面积是多少?
的面积最小?最小面积是多少?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1 , C2的极坐标方程分别为ρ=2cosθ, ![]() ,射线θ=φ,
,射线θ=φ, ![]() ,
, ![]() 与曲线C1交于(不包括极点O)三点A,B,C.
与曲线C1交于(不包括极点O)三点A,B,C.
(Ⅰ)求证: ![]() ;
;
(Ⅱ)当 ![]() 时,求点B到曲线C2上的点的距离的最小值.
时,求点B到曲线C2上的点的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}中,定义:dn=an+2+an﹣2an+1(n≥1),a1=1.
(1)若dn=an , a2=2,求an;
(2)若a2=﹣2,dn≥1,求证此数列满足an≥﹣5(n∈N*);
(3)若|dn|=1,a2=1且数列{an}的周期为4,即an+4=an(n≥1),写出所有符合条件的{dn}.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在无穷数列![]() 中,
中, ![]() ,对于任意
,对于任意![]() ,都有
,都有![]() ,
, ![]() .设
.设![]() ,记使得
,记使得![]() 成立的n的最大值为
成立的n的最大值为![]() .
.
(Ⅰ)设数列{an}为1,3,5,7,…,写出b1,b2,b3的值;
(Ⅱ)若{an}为等比数列,且a2=2,求b1+b2+b3+…+b50的值;
(Ⅲ)若{bn}为等差数列,求出所有可能的数列{an}.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,AB=![]() ,BC=1,P为△ABC内一点,∠BPC=90°.
,BC=1,P为△ABC内一点,∠BPC=90°.
(1)若PB=![]() ,求PA;
,求PA;
(2)若∠APB=150°,求tan∠PBA.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com