平面与平面垂直的性质定理可简言：面面垂直，则线面垂直．两平面垂直会有许多性质，选取这条性质作为性质定理有什么意义？这条定理都有什么应用？
|
我们已经会判断两个平面互相垂直，除定义外，还可用“一个平面经过另一个平面的一条垂线，那么这两个平面垂直”来判定两个平面垂直．两个相交平面相联系的最重要的纽带莫过于它们之间的交线了，所以两垂直平面的性质问题的关键就在于交线及与交线垂直的直线上． 性质定理：两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直． 不难证明这个定理的逆命题，即如果一个平面内垂直于交线的任意一条直线与另一个平面垂直，则这两个平面垂直．也就是说平面与平面垂直的性质定理是两个相垂直的平面区别于其他两个相交平面的特有的性质． |
|
这个定理为证明线面垂直提供了思路：只要有两个平面垂直，那么向交线作垂线便得线面垂直，进一步便有线与线的垂直．平面与平面垂直的判定与性质相互结合，为证明线线垂直、线面垂直提供了更多的技巧． |
激活思维优加课堂系列答案
活力试卷系列答案
课课优能力培优100分系列答案科目：高中数学 来源：2011-2012学年山东省高三下学期模拟预测理科数学试卷（解析版） 题型：解答题
在四棱锥
中，
平面
，底面为矩形，
.
（Ⅰ）当
时，求证：
；
（Ⅱ）若
边上有且只有一个点
，使得
，求此时二面角
的余弦值.
【解析】第一位女利用线面垂直的判定定理和性质定理得到。当a=1时，底面ABCD为正方形，
又因为
,
………………2分
又
，得证。
第二问，建立空间直角坐标系，则B(1,0,1)D(0,a,0)C(1,a,0)P(0,0,1)……4分
设BQ=m，则Q(1，m,0)(0《m《a》
要使
，只要
所以
，即
………6分
由此可知时，存在点Q使得
当且仅当m=a-m，即m=a/2时，BC边上有且只有一个点Q，使得
由此知道a=2, 设平面POQ的法向量为
,所以
平面PAD的法向量
则
的大小与二面角A-PD-Q的大小相等所以
因此二面角A-PD-Q的余弦值为
解：(Ⅰ)当时，底面ABCD为正方形，
又因为,又
………………3分
(Ⅱ) 因为AB,AD,AP两两垂直，分别以它们所在直线为X轴、Y轴、Z轴建立坐标系，如图所示，
则B(1,0,1)D(0,a,0)C(1,a,0)P(0,0,1)…………4分
设BQ=m，则Q(1，m,0)(0《m《a》要使，只要
所以，即………6分
由此可知时，存在点Q使得
当且仅当m=a-m，即m=a/2时，BC边上有且只有一个点Q，使得由此知道a=2,
设平面POQ的法向量为
,所以 平面PAD的法向量
则的大小与二面角A-PD-Q的大小相等所以
因此二面角A-PD-Q的余弦值为
查看答案和解析>>
科目：高中数学 来源：2013届浙江省高二下学期期中理科数学试卷（解析版） 题型：解答题
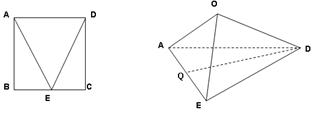
如图，边长为2的正方形ABCD，E是BC的中点，沿AE，DE将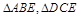
折起，使得B与C重合于O．
（Ⅰ）设Q为AE的中点，证明：QD
AO；
（Ⅱ）求二面角O—AE—D的余弦值．
【解析】第一问中，利用线线垂直，得到线面垂直，然后利用性质定理得到线线垂直。取AO中点M，连接MQ，DM，由题意可得：AO
EO, DOEO，
AO=DO=2．AODM
因为Q为AE的中点，所以MQ//E0,MQAO
AO平面DMQ,AODQ
第二问中，作MNAE,垂足为N，连接DN
因为AOEO, DOEO，EO平面AOD，所以EODM
，因为AODM ，DM平面AOE
因为MNAE，DNAE, 
DNM就是所求的DM=
，MN=
,DN=
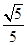,COSDNM=
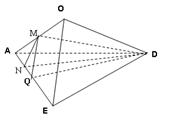
（1）取AO中点M，连接MQ，DM，由题意可得：AOEO, DOEO，
AO=DO=2．AODM
因为Q为AE的中点，所以MQ//E0,MQAO
AO平面DMQ,AODQ
（2）作MNAE,垂足为N，连接DN
因为AOEO, DOEO，EO平面AOD，所以EODM
，因为AODM ，DM平面AOE
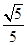因为MNAE，DNAE, DNM就是所求的DM=，MN=,DN=,COSDNM=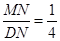
二面角O-AE-D的平面角的余弦值为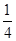
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com