已知函数f(x)=xlnx,g(x)=-x2+ax-2.
(1)求函数f(x)在[t,t+2](t>0)上的最小值;
(2)若函数y=f(x)与y=g(x)的图象恰有一个公共点,求实数a的值;
(3)若函数y=f(x)+g(x)有两个不同的极值点x1,x2(x1<x2),且x2-x1>ln2,求实数a的取值范围.
解:(1)由f′(x)=lnx+1=0,可得x=

∴①
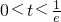
时,函数f(x)在(t,

)上单调递减,在(

,t+2)上单调递增
∴函数f(x)在[t,t+2](t>0)上的最小值为
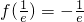
;
②当t≥

时,f(x)在[t,t+2]上单调递增,∴f(x)
min=f(t)=tlnt,
∴f(x)
min=
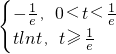
;
(2)函数y=f(x)与y=g(x)的图象恰有一个公共点,等价于f(x)-g(x)=xlnx+x
2-ax+2=0在(0,+∞)上有且只有一根,即a=
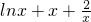
在(0,+∞)上有且只有一根
令h(x)=
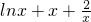
,则
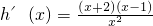
∴x∈(0,1)时,h′(x)<0,函数单调递减;x∈(1,+∞)时,h′(x)>0,函数单调递增
∴a=h(x)
min=h(1)=3
(3)y=f(x)+g(x)=xlnx-x
2+ax-2,则y′=lnx-2x+1+a
题意即为y′=lnx-2x+1+a=0有两个不同的实根x
1,x
2(x
1<x
2),
即a=-lnx+2x-1有两个不同的实根x
1,x
2(x
1<x
2),
等价于直线y=a与函数G(x)=-lnx+2x-1的图象有两个不同的交点
∵
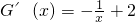
,∴G(x)在(0,

)上单调递减,在(

,+∞)上单调递增
画出函数图象的大致形状(如右图),
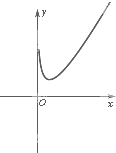
由图象知,当a>G(x)
min=G(

)=ln2时,x
1,x
2存在,且x
2-x
1的值随着a的增大而增大
而当x
2-x
1=ln2时,由题意
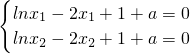
两式相减可得

∴x
2=4x
1代入上述方程可得
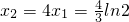
此时
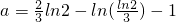
所以,实数a的取值范围为
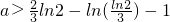
.
分析:(1)求导数,再分类讨论,确定函数在区间上的单调性,即可求得函数的最小值;
(2)将函数图象只有一个公共点转化为方程只有一根,再分离参数,求出函数的最小值即可;
(3)函数由两个不同的极值点转化为导函数等于0的方程有两个不同的实数根,进而转化为图象的交点问题,由此可得结论.
点评:本题考查导数知识的运用,考查函数的单调性与最值,考查分离参数法的运用,考查数形结合的数学思想,综合性强.


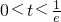 时,函数f(x)在(t,
时,函数f(x)在(t, )上单调递减,在(
)上单调递减,在( ,t+2)上单调递增
,t+2)上单调递增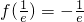 ;
; 时,f(x)在[t,t+2]上单调递增,∴f(x)min=f(t)=tlnt,
时,f(x)在[t,t+2]上单调递增,∴f(x)min=f(t)=tlnt,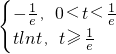 ;
;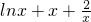 在(0,+∞)上有且只有一根
在(0,+∞)上有且只有一根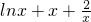 ,则
,则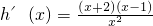
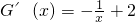 ,∴G(x)在(0,
,∴G(x)在(0, )上单调递减,在(
)上单调递减,在( ,+∞)上单调递增
,+∞)上单调递增
 )=ln2时,x1,x2存在,且x2-x1的值随着a的增大而增大
)=ln2时,x1,x2存在,且x2-x1的值随着a的增大而增大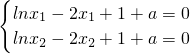

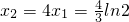
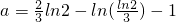
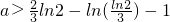 .
.

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<