
【题目】如图,在直角梯形ABCD中,AB∥DC,AE⊥DC,BE∥AD.M、N分别是AD、BE上的点,且AM=BN,将三角形ADE沿AE折起,则下列说法正确的是 (填上所有正确说法的序号).
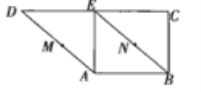
①不论D折至何位置(不在平面ABC内)都有MN∥平面DEC;
②不论D折至何位置都有MN⊥AE;
③不论D折至何位置(不在平面ABC内)都有MN∥AB;
④在折起过程中,一定存在某个位置,使EC⊥AD.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】在一次购物抽奖活动中,假设某10张券中有一等奖1张,可获价值50元的奖品;有二等奖券3张,每张可获价值10元的奖品;其余6张没有将;某顾客从此10张券中任取2张,求:
(1)该顾客中奖的概率;
(2)该顾客获得的奖品总价值![]() (元)的概率分布列.
(元)的概率分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
等腰梯形ABEF中,AB∥EF,AB=2,AD=AF=1,AF⊥BF,O为AB的中点,矩形ABCD 所在的平面和平面ABEF互相垂直.
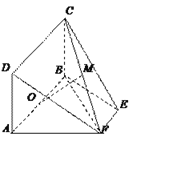
(1)求证:AF⊥平面CBF;
(2)设FC的中点为M,求证:OM∥平面DAF;
(3)求三棱锥C-BEF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-5:不等式选讲
已知函数f(x)=|2x+1|+|2x-a|.
(I)若f(x)的最小值为2,求a的值;
(II)若f(x)≤|2x-4|的解集包含[-2,-1],求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为考察某种药物预防禽流感的效果,进行动物家禽试验,调查了100个样本,统计结果为:服用药的共有60个样本,服用药但患病的仍有20个样本,没有服用药且未患病的有20个样本.
(1)根据所给样本数据完成下面2×2列联表;
(2)请问能有多大把握认为药物有效?
不得禽流感 | 得禽流感 | 总计 | |
服药 | |||
不服药 | |||
总计 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于命题![]() :存在一个常数
:存在一个常数![]() ,使得不等式
,使得不等式![]() 对任意正数
对任意正数![]() ,
,![]() 恒成立.
恒成立.
(1)试给出这个常数![]() 的值;
的值;
(2)在(1)所得结论的条件下证明命题![]() ;
;
(3)对于上述命题,某同学正确地猜想了命题![]() :“存在一个常数
:“存在一个常数![]() ,使得不等式
,使得不等式![]() 对任意正数
对任意正数![]() ,
,![]() ,
,![]() 恒成立.”观察命题
恒成立.”观察命题![]() 与命题
与命题![]() 的规律,请猜想与正数
的规律,请猜想与正数![]() ,
,![]() ,
,![]() ,
,![]() 相关的命题.
相关的命题.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为招聘新员工设计了一个面试方案:应聘者从6道备选题中一次性随机抽取3道题,按题目要求独立完成.规定:至少正确完成其中2道题的便可通过.已知6道备选题中应聘者甲有4道题能正确完成,2道题不能完成;应聘者乙每题正确完成的概率都是![]() ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.
(1)分别求甲、乙两人正确完成面试题数的分布列及数学期望;
(2)请分析比较甲、乙两人谁面试通过的可能性大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com