
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且2,
,且2,![]() ,
,![]() 成等差数列.
成等差数列.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)对于(2)中的![]() ,设
,设![]() ,求数列
,求数列![]() 中的最大项.
中的最大项.
科目:高中数学 来源: 题型:
【题目】为调查乘客的候车情况,公交公司在某站台的60名候车乘客中随机抽取15人,将他们的候车时间(单位:分钟)作为样本分成5组,如表所示:
组别 | 候车时间 | 人数 |
一 |
| 2 |
二 |
| 6 |
三 |
| 4 |
四 |
| 2 |
五 |
| 1 |
(1)估计这60名乘客中候车时间少于10分钟的人数;
(2)若从上表第三、四组的6人中随机抽取2人作进一步的问卷调查,求抽到的两人恰好来自同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
在如图所示的多面体中,四边形![]() 和
和![]() 都为矩形。
都为矩形。

(Ⅰ)若![]() ,证明:直线
,证明:直线![]() 平面
平面![]() ;
;
(Ⅱ)设![]() ,
, ![]() 分别是线段
分别是线段![]() ,
, ![]() 的中点,在线段
的中点,在线段![]() 上是否存在一点
上是否存在一点![]() ,使直线
,使直线![]() 平面
平面![]() ?请证明你的结论。
?请证明你的结论。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加环保知识竞赛的1200名学生中,随机抽取60名,将其成绩(均为整数)分成六段![]() ,
,![]() ,…,
,…,![]() 后画出如图的频率分布直方图.
后画出如图的频率分布直方图.
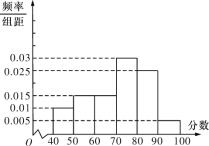
(1)估计这次竞赛成绩的众数与中位数(结果保留小数点后一位);
(2)若这次竞赛成绩不低于80分的同学都可以获得一份礼物,试估计该校参加竞赛的1200名学生中可以获得礼物的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 上一点
上一点![]() 到其焦点的距离为
到其焦点的距离为![]() .
.
(1)求![]() 与
与![]() 的值;
的值;
(2)若斜率为![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 为抛物线
为抛物线![]() 上一点,其横坐标为1,记直线
上一点,其横坐标为1,记直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,试问:
,试问:![]() 是否为定值?并证明你的结论.
是否为定值?并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
设![]() 是函数
是函数![]() 的图象上任意两点,且
的图象上任意两点,且![]() ,已知点
,已知点![]() 的横坐标为
的横坐标为![]() .
.
(1)求证:![]() 点的纵坐标为定值;
点的纵坐标为定值;
(2)若![]() 求
求![]() ;
;
(3)已知![]() =
= ,其中
,其中![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和,若
项和,若![]() 对一切
对一切![]() 都成立,试求
都成立,试求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() .
.
(1)求f(2)+f(![]() ),f(3)+f(
),f(3)+f(![]() )的值;
)的值;
(2)求证:f(x)+f(![]() )是定值;
)是定值;
(3)求f(2)+f(![]() )+f(3)+f(
)+f(3)+f(![]() )+…+f(2012)+f(
)+…+f(2012)+f(![]() )的值.
)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com