
【题目】某化工厂生产某种产品,当年产量在150吨至250吨时,每年的生产成本y万元与年产量x吨之间的关系可可近似地表示为y= ![]() ﹣30x+4000.
﹣30x+4000.
(1)若每年的生产总成本不超过2000万元,求年产量x的取值范围;
(2)求年产量为多少吨时,每吨的平均成本最低,并求每吨的最低成本.
【答案】
(1)解:由题意可得 ![]() ﹣30x+4000≤2000,解得100≤x≤200,
﹣30x+4000≤2000,解得100≤x≤200,
∵当年产量在150吨至250吨时,每年的生产成本y万元与年产量x吨之间的关系
可近似地表示为y= ![]() ﹣30x+4000,
﹣30x+4000,
∴150≤x≤200,
故每年的生产总成本不超过2000万元,年产量x的取值范围为[150,200]
(2)解:依题意,每吨平均成本为 ![]() (万元),
(万元),
则 ![]() =
= ![]() +
+ ![]() ﹣30≥2
﹣30≥2 ![]() ﹣30=10
﹣30=10
当且仅当x=200时取等号,又150<200<250,
所以年产量为200吨时,每吨平均成本最低,每吨的最低成本10万元.
【解析】(1)根据题意使得成本不超过2000万元,列出不等式,求解不等式得到年产量x的范围,(2)表示出每吨平均成本为![]() ,利用均值不等式得到x的取值,故每吨最低成本为10万元.
,利用均值不等式得到x的取值,故每吨最低成本为10万元.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
【题目】函数f(x)= ![]() +
+ ![]() 的定义域为( )
的定义域为( )
A.[﹣1,2)∪(2,+∞)
B.[﹣1,+∞)
C.(﹣∞,2)∪(2,+∞)
D.(﹣1,2)∪(2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={x|(x﹣2m+1)(x﹣m+2)<0},B={x|1≤x+1≤4}.
(1)若m=1,求A∩B;
(2)若A∩B=A,求实数m的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据所学知识完成题目:
(1)若a、b、m、n∈R+ , 求证: ![]() ;
;
(2)利用(1)的结论,求下列问题:已知 ![]() ,求
,求 ![]() 的最小值,并求出此时x的值.
的最小值,并求出此时x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一艘船在航行过程中发现前方的河道上有一座圆拱桥.在正常水位时,拱桥最高点距水面8m,拱桥内水面宽32m,船只在水面以上部分高6.5m,船顶部宽8m,故通行无阻,如图所示. 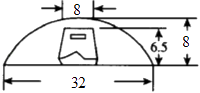
(1)建立适当的平面直角坐标系,求正常水位时圆弧所在的圆的方程;
(2)近日水位暴涨了2m,船已经不能通过桥洞了.船员必须加重船载,降低船身在水面以上的高度,试问:船身至少降低多少米才能通过桥洞?(精确到0.1m, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】满足不等式|x﹣A|<B(B>0,A∈R)的实数x的集合叫做A的B邻域,若a+b﹣2的a+b邻域是一个关于原点对称的区间,则 ![]() 的取值范围是 .
的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】仙游某家具城生产某种家具每件成本为3万元,每件售价为x万元(x>3),月销量为t件,经验表明,t= ![]() +10(x﹣6)2 , 其中3<x<6,a为常数.已知销售价格为5万元时,月销量为11件.
+10(x﹣6)2 , 其中3<x<6,a为常数.已知销售价格为5万元时,月销量为11件.
(1)求a的值;
(2)求售价定为多少时,该家具的月利润最大,最大值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的不等式(kx﹣k2﹣4)(x﹣4)>0,其中k∈R;
(1)当k=4时,求上述不等式的解集;
(2)当上述不等式的解集为(﹣5,4)时,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数y=f(x),f(0)≠0,当x>0时,f(x)>1,对任意的a,b∈R都有f(a+b)=f(a)f(b)且对任意的x∈R,恒有f(x)>0;
(1)求f(0);
(2)证明:函数y=f(x)在R上是增函数;
(3)若f(x)f(2x﹣x2)>1,求x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com